RStudio Quick Reference

Loading Mosaic and MosaicCalc Packages

Run the following code block to load the mosaic and mosaicCalc libraries

knitr::opts_chunk$set(echo = TRUE)
suppressPackageStartupMessages(library(mosaic))
suppressPackageStartupMessages(library(mosaicCalc))

Troubleshooting

Without fail, you will run into problems. Sometimes RStudio will give you helpful error messages, but sometimes they are obtuse. Here’s a list of some common errors and what might be wrong:

  • Nothing ran, all I got was a plus sign… You probably forgot some parentheses. Try the following:

    • Enter a parenthesis on that line to see if this closes it out.
    • Press the Escape key to get to a new line.

  • Unexpected symbol in… You may have forgotten a multiplication sign or otherwise gave RStudio a symbol it cannot parse. Check your line of code again to see if you have all your symbols.

  • Object not found… You may not have defined that variable (or function) yet. Check your environment tab to see if it has the object you’re looking for (or if you’ve called it something different than you remember!). You also may be trying to use something from a data set that you have not included as a parameter. See if you need to add in the parameter data=....

  • Could not find function… RStudio doesn’t know what function you’re using. Check your capitalization and that you have the right packages installed.

  • … number of items to replace is not a multiple of replacement length … Your input variable doesn’t match the name variable you used in the output when you called makeFun. Maybe you used x on one side of the tilde ~ and t on the other side?

  • Argument “name” is missing, with no default… You’re probably trying to use makeFun without loading the mosaic package, or to take a derivative or antiderivative without the mosaicCalc package. See the “Loading Mosaic and MosaicCalc Packages” section at the top of this page for how to fix this.

  • I can’t find my data! You may have fetched it but did not give it a name. Go back to your fetch command and make sure you have assigned it a variable.

Functions and Data

Common Functions

function R command comments
\(x^2\) x^2
\(4x^2 -7x + 3\) 4*x^2 - 7*x + 3 You must always include the * when you multiply
\(\sqrt{x}\) sqrt(x) or x^(1/2)
\(\sqrt[3]{x}\) x^(1/3)
\(\sin(x)\) sin(x)
\(\cos(x)\) cos(x)
\(e^x\) exp(x) exp is a function (like sin and cos), so you do NOT need a ^
\(\mbox{ln}(x)\) log(x) RStudio uses the natural logarithm as the default
\(\log(x) = \log_{10}(x)\) log10(x) Humans default to “log base 10.” RStudio does not!
\(\log_{b}(x)\) log(x,b) You can use any number \(b\) as the base for your logarithm

Defining Your Own Function

The makeFun command is part of the mosaic package.

desired function R command comments
\(f(x) = x^2 +5x + 6\) f = makeFun(x^2 + 5*x + 6 ~ x) remember your * signs!
\(g(x) = \sin^2(x) - \frac{1}{2}\) g = makeFun(sin(x)^2 - 1/2 ~ x) note the placement of ^2
\(P(t) = 5 e^{.25 t}\) P = makeFun(5 * exp(0.25 * t) ~ t) exp does not need a ^
\(Q(t) = 12.38 (1.041)^t\) Q = makeFun(12.38 * (1.041)^t ~ t)

Notes:

  • The general syntax is makeFun( OUTPUT ~ INPUT ) where the OUTPUT is a function of the INPUT.
  • You must assign this to a variable so that you can use it later. So your command must start with f = ... so that you get a function named f.
  • The variable (x or t, etc) that appears in the OUTPUT must match the INPUT variable that appears after the tilde ~. The the command makeFun(x^2 ~ t) won’t work because the x^2 is not a function of t.

Creating Lists of Data

Use c() to “combine” some values into a list. Assign the list to a variable so that you can use it later.

my_primes = c(2, 3, 5, 7, 11, 13, 17, 19, 23, 29)
my_primes
##  [1]  2  3  5  7 11 13 17 19 23 29
my_data = c(5, -2, 7, 3, -10, 15)
my_data
## [1]   5  -2   7   3 -10  15

Use seq() to generate a sequential list of values in a specified range. The optional third parameter tells RStudio to increment by that value instead of incrementing by 1.

my_seq1 = seq(1,10)
my_seq1
##  [1]  1  2  3  4  5  6  7  8  9 10
my_seq2 = seq(5, 6, 0.25)
my_seq2
## [1] 5.00 5.25 5.50 5.75 6.00
my_seq3 = seq(5, 6, 0.1)
my_seq3
##  [1] 5.0 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 6.0

Plotting Data

Use gf_point to plot a list of \(y\)-axis data versus a list of \(x\)-axis data. Separate these lists with a tilde ~.

X = seq(1:5)
Y = X^2
gf_point(Y ~ X)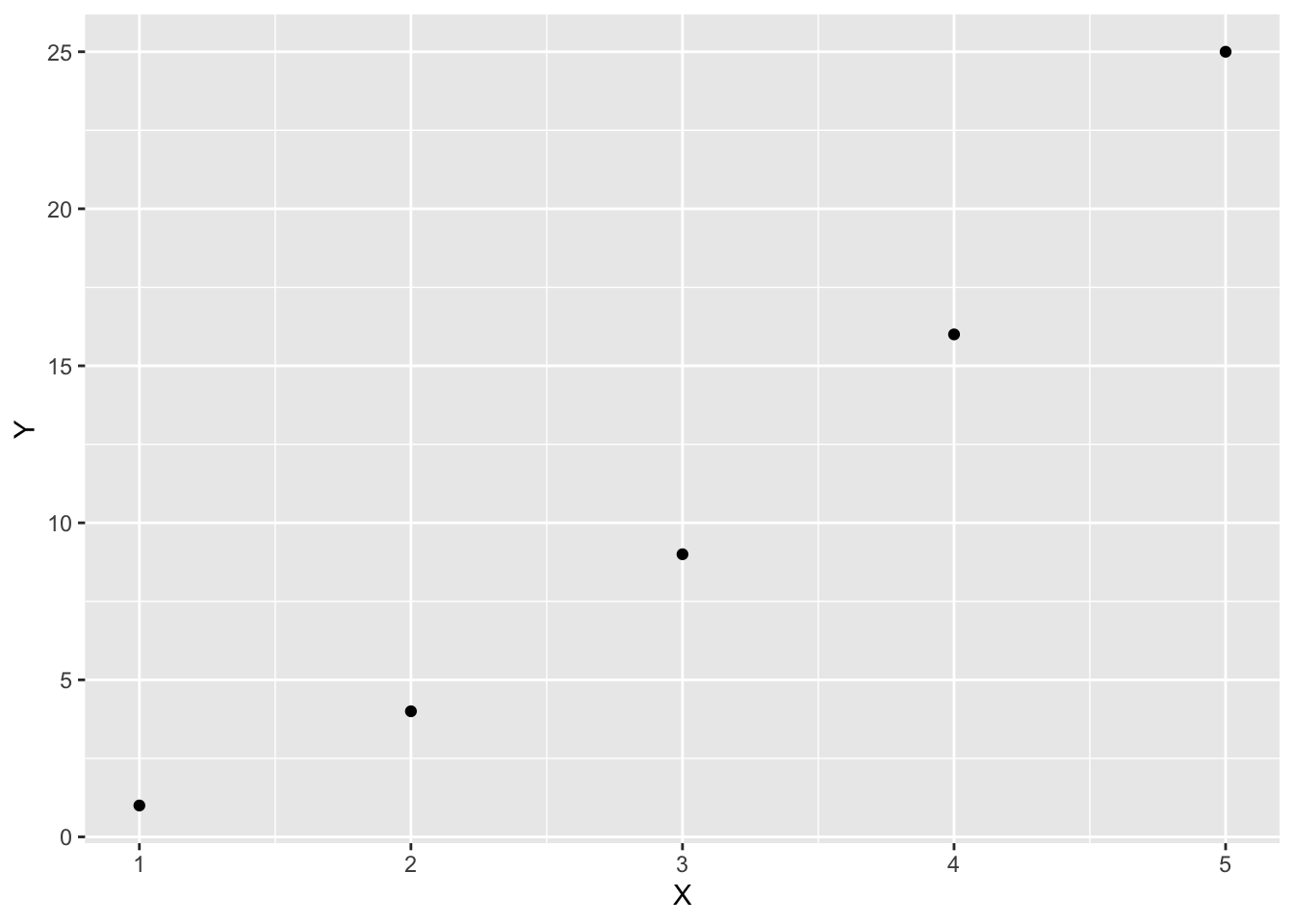

The prefix gf in the name gf_point is short for “graph formula.” You can specify labels for the horizontal axis and the vertical axis using xlab and ylab.

x_data = c(2,3,5,8,13)
y_data = c(2,4,8,4,2)
gf_point(y_data ~ x_data, xlab='day', ylab='rainfall (mm)')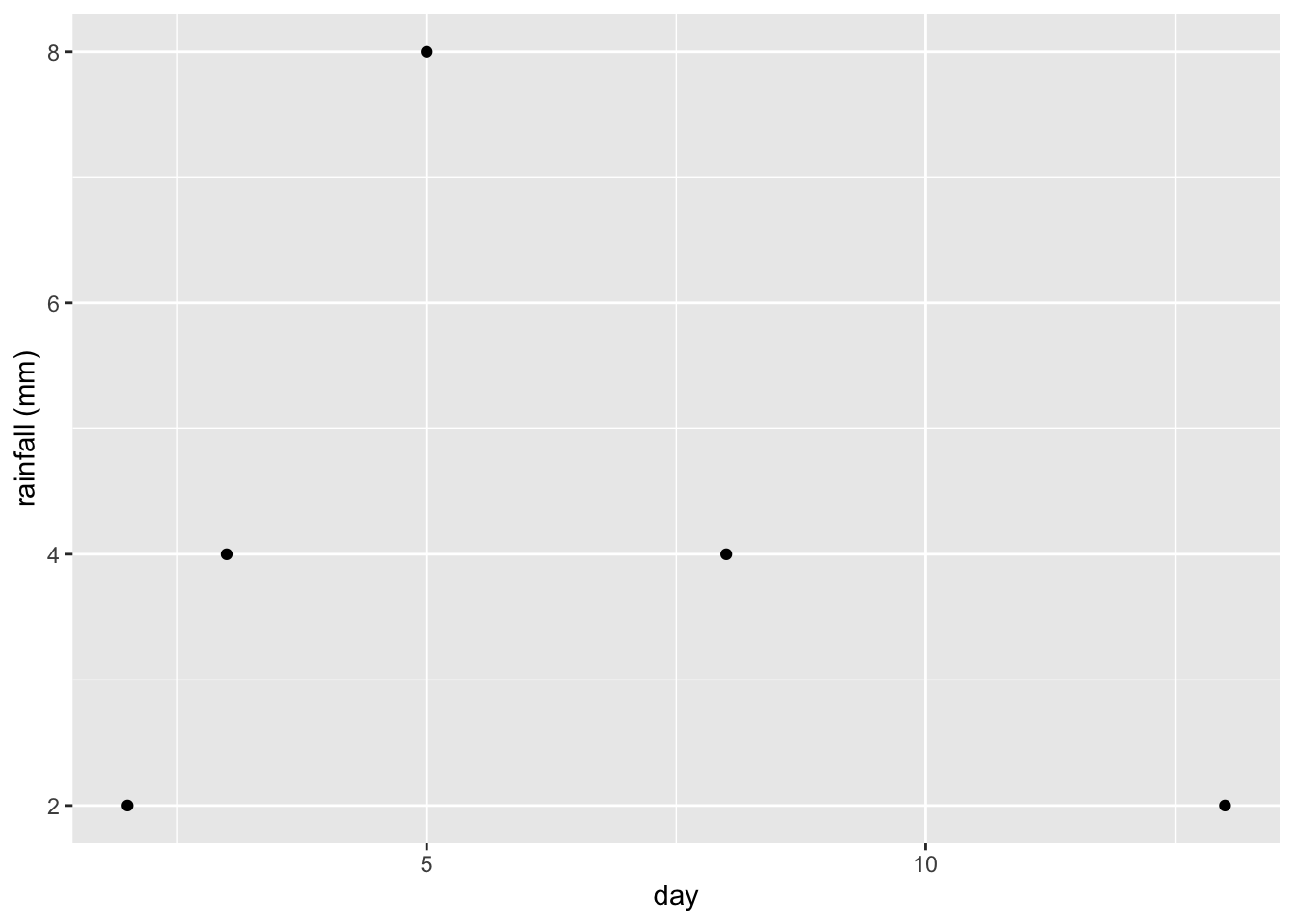

Plotting Functions

Use slice_plot to plot a function.

  • As with gf_point, we use a tilde ~ to separate the output variable (the function) from the input variable.
  • The required domain argument specifies the domain for the plot.
slice_plot(sin(x) ~ x, domain(x=0:2*pi), color='blue')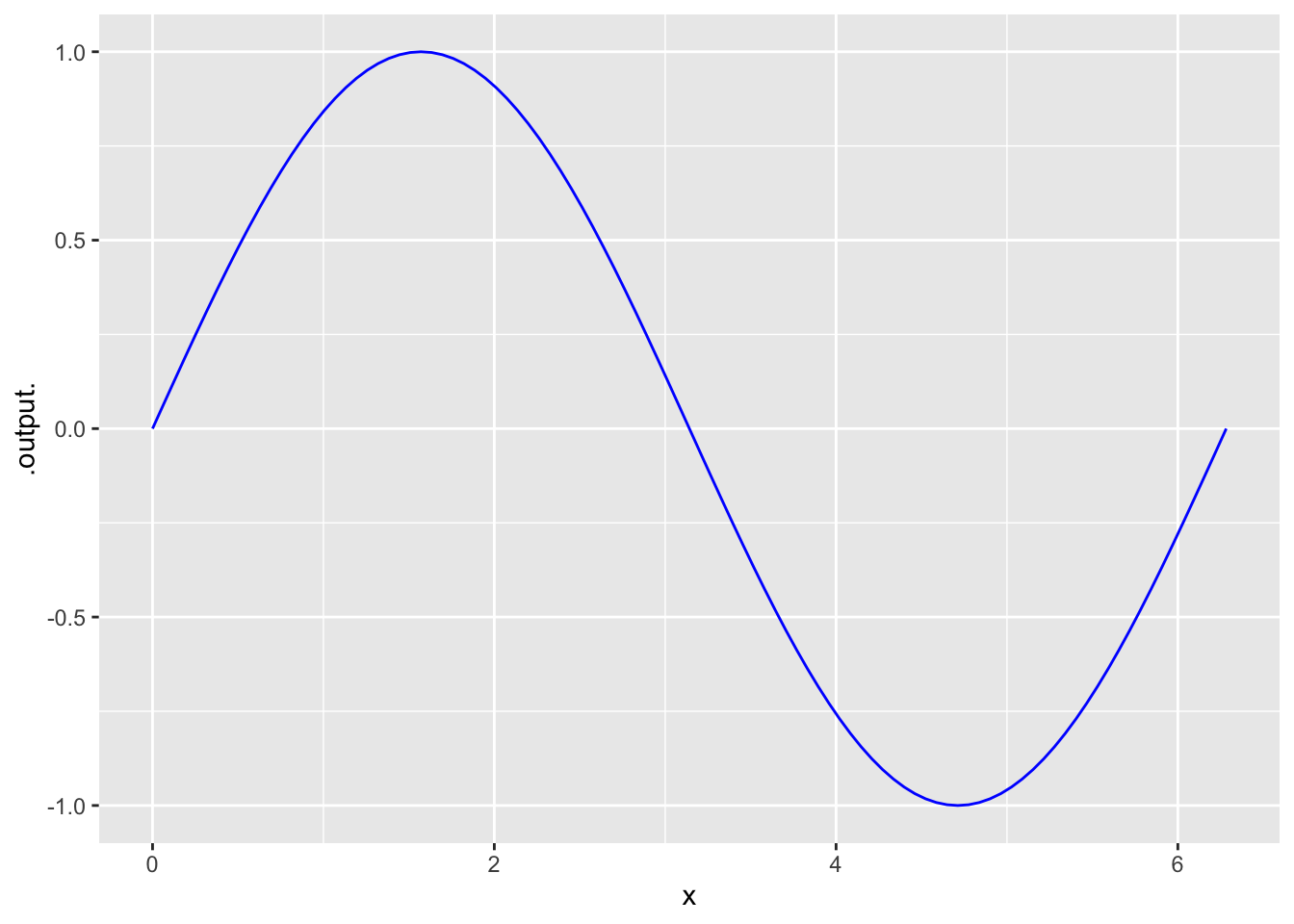

You can add a label to the plot, or to the axes. You do this by

slice_plot(sin(x) ~ x, domain(x=0:2*pi), color='blue') + 
  ylab('sin(x)') + xlab('x values') + labs(title="y=sin(x)")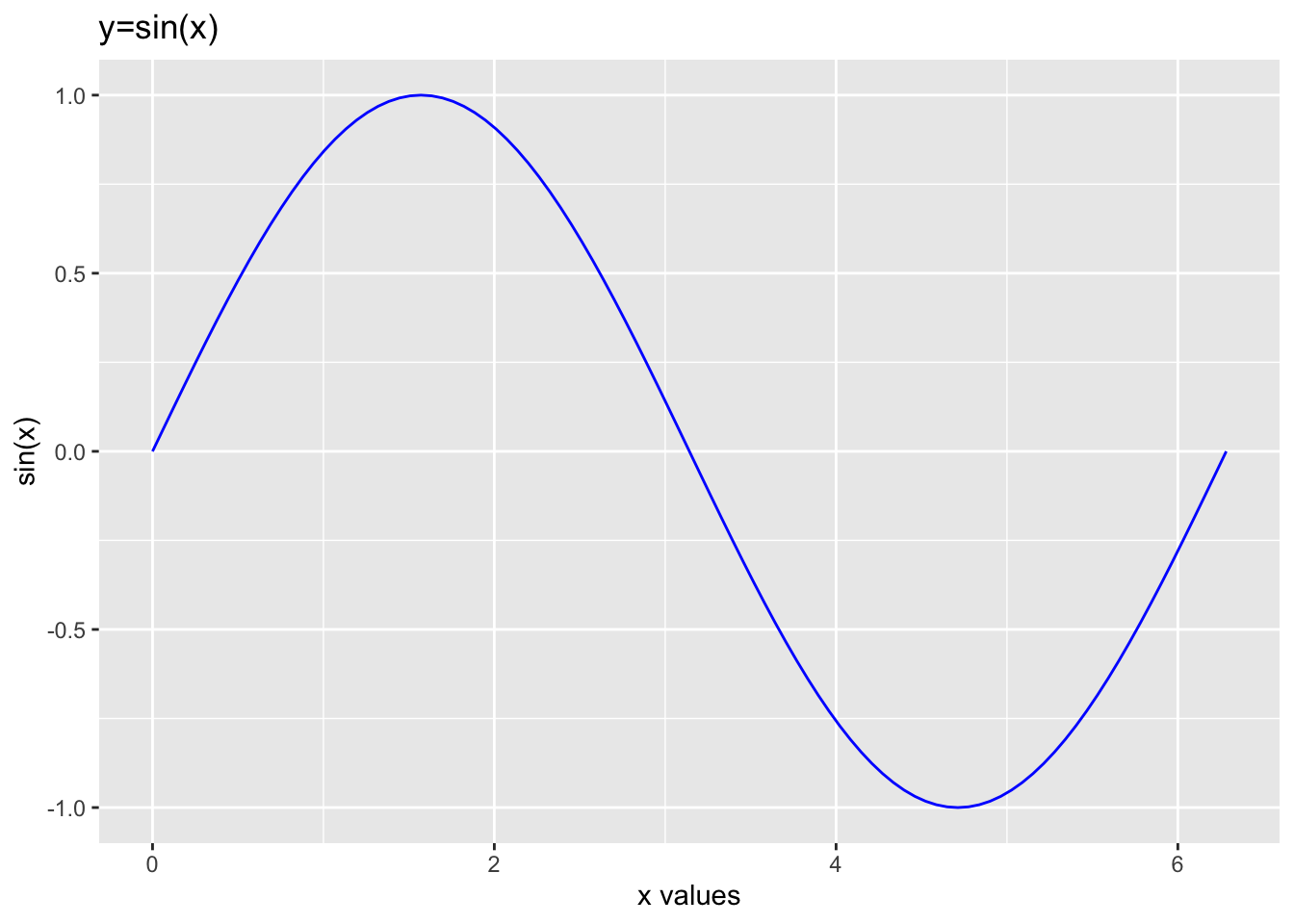

We can layer one plot on top of another by using a pipe %>%.

  • You only need to specify the domain for the first plot because the second one is added to the first.
  • It’s helpful to change the color for subsequent plots. Use the argument color="red" using any color name you like (RStudio knows a lot of colors!)
slice_plot(2 * sin(x) ~ x, domain(x=0:2*pi)) %>%
slice_plot(cos(3*x) ~ x, color='green')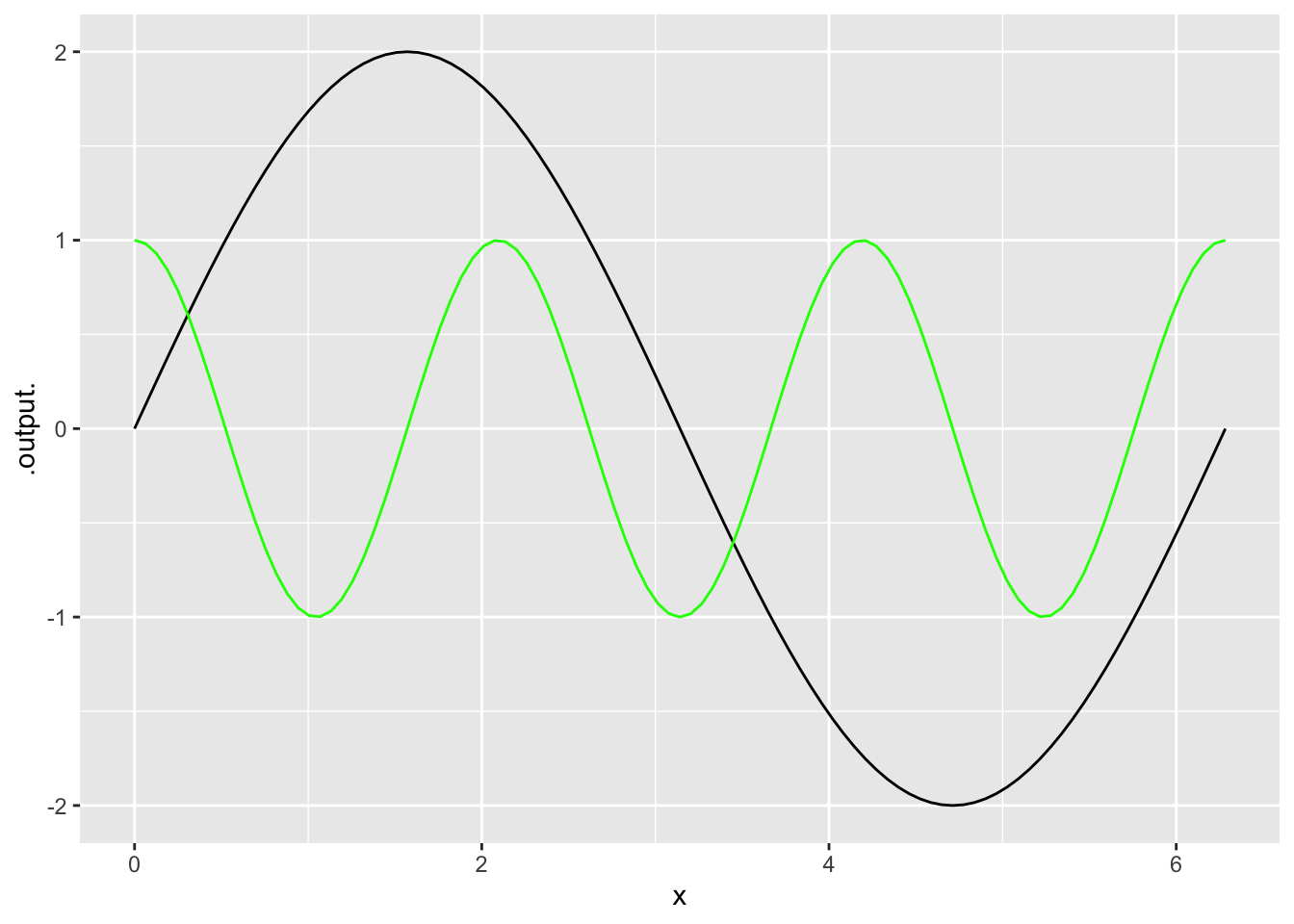

  • The %>% symbol is pronounced “pipe.” The pipe must appear at the end of the line (not at the start of the next line).
  • A command involving a pipe is called a “pipeline.” Think of the calculation as flowing from one command to the next, left to right.
  • If you have specified the domain() at an early stage in the pipeline, you don’t need to specify it again in the later plotting commands. But, if you want, feel free to set the domain explicitly. This is helpful if you want the graphics domain to be different for the different layers.
  • Pro Tip: write a pipeline with one line for each stage, with the pipe symbol at the end of each stage.

The slice_plot command takes a whole variety of parameters, here are a few useful ones:

  • domain: sets the range of your \(x\)-axis. Example: domain(x=1:4).
  • color: sets the color of the function you plot. RStudio will recognize most basic colors, which you will pass as strings. Example: color="red".

Let’s try some of this out. I broke the third line so it would all fit, you don’t need to!

f=makeFun(x^3+3~x)
g=makeFun(3*x^2~x)
slice_plot(f(x)~x, domain(x=1:4), color="blue") %>%
slice_plot(g(x)~x, col="red") + xlab("time")  + ylab("red=velocity, blue=position")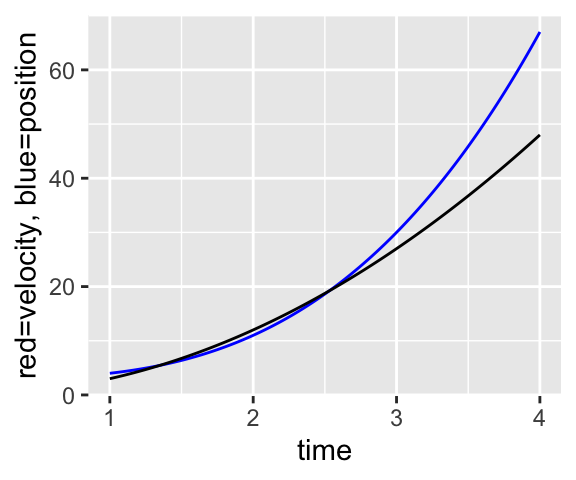

RStudio is a little weird about plots in the RMarkdown in that you might get multiples if you’re adding plots together. If you want the chunk to hold all plots until the end, add fig.show='hold' into the script braces at the top of the chunk.

Plotting Data and Functions

We can also combine plots of data and functions using the pipe comment >%>.

time_data = seq(0,50, 10)
pop_data = c(6.82, 9.63, 14.3, 20.48, 28.94, 42.25)

P = makeFun( 6.82 * (1.037)^t ~ t)

gf_point(pop_data ~ time_data, xlab='years since 1950', ylab='population (millions)') %>%
slice_plot(P(t) ~ t, domain(t=0:50), color='orange')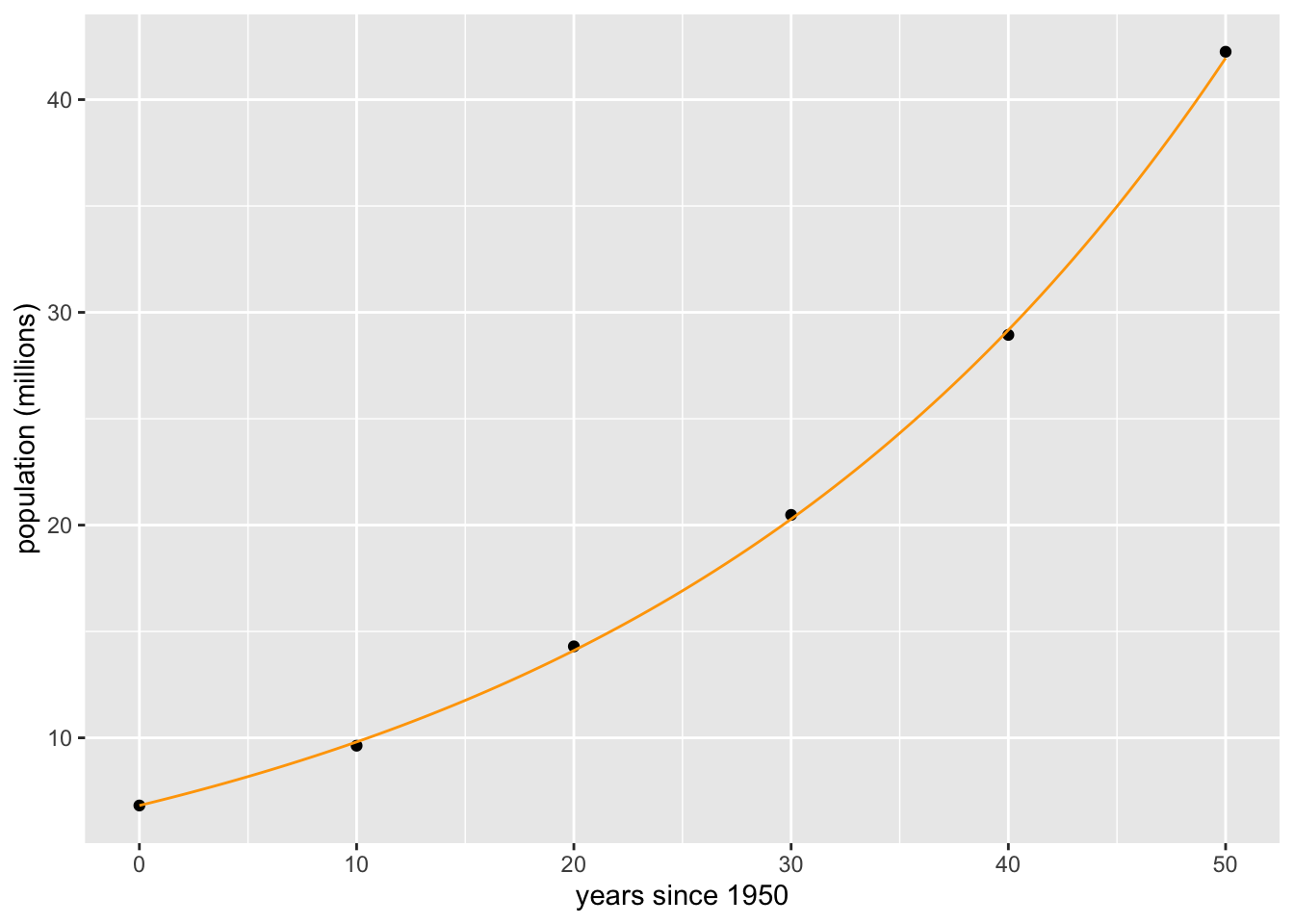

Fitting a Function to Data

The fitModel command is part of the mosaic package. Here is how you would fit a linear model to data

xdata = c(1,2,3,4,5)
ydata = c(5.3, 7.7, 10.1, 11.3, 12.0    )

fitModel(ydata  ~ A* xdata  + B)
## function (xdata, ..., transformation = function (x) 
## x) 
## return(transformation(predict(model, newdata = data.frame(xdata = xdata), 
##     ...)))
## <environment: 0x7fcda68e0f20>
## attr(,"coefficients")
##    A    B 
## 1.70 4.18 
## attr(,"class")
## [1] "nlsfunction" "function"

This output says that the best fitting linear function has slope \(A=1.70\) and \(y\)-intercept \(B=4.18\). So let’s create the corresponding linear function and plot it with the data.

f = makeFun(1.70 *  x + 4.18 ~ x)

gf_point(ydata ~ xdata) %>%
slice_plot(f(x) ~ x, domain(x=1:5), color='orange')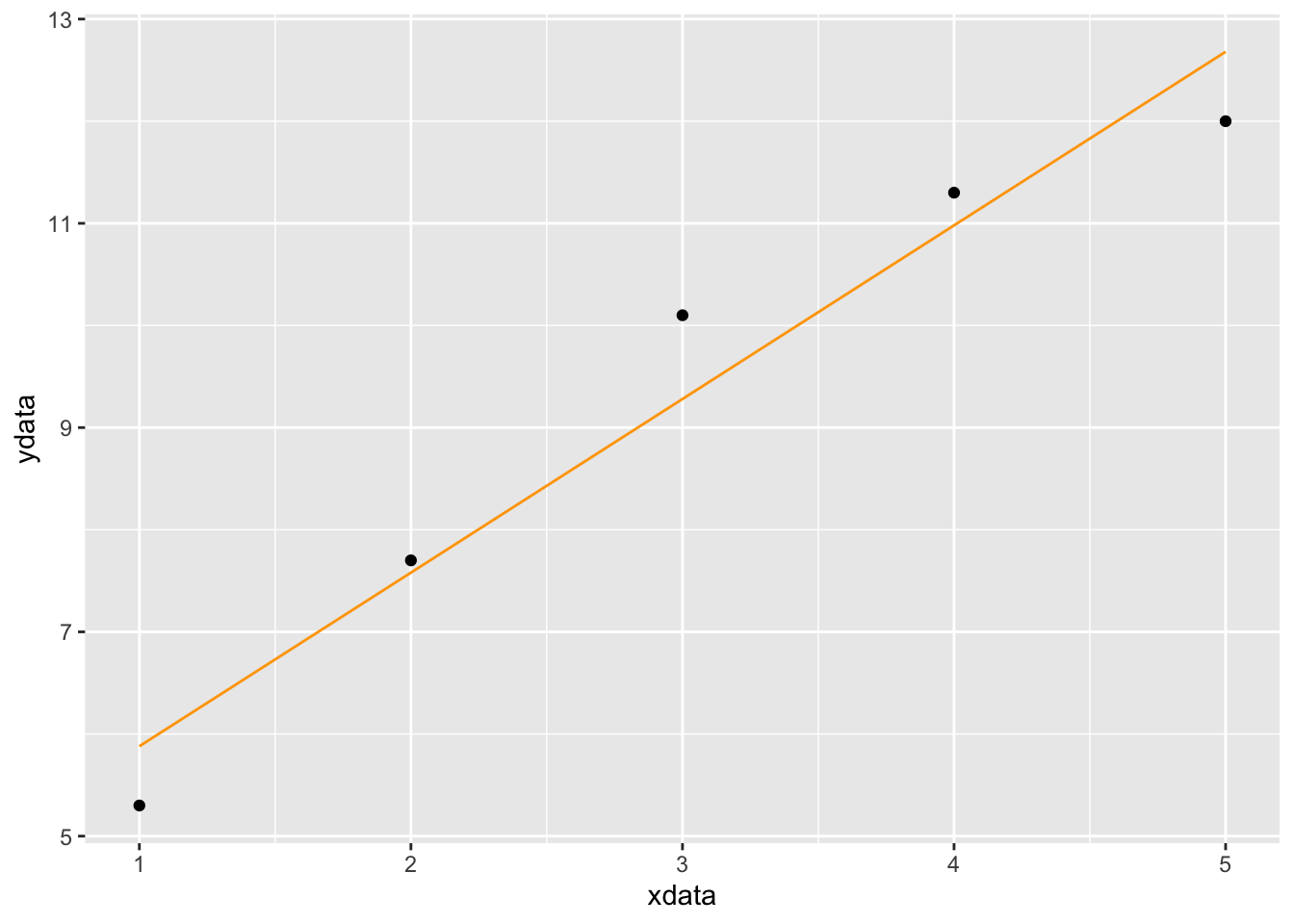

Fitting a Power Function to Data

Here are the steps to fit xdata and ydata to a power function \(f(x) = c x^p\).

  1. Take the log of both xdata and ydata
  2. Fit a linear function \(y = A x + B\) to the resulting data
  3. The original constants are p = A and c = exp(B)

Here is an example

f = makeFun(4.3 * x^(1.7)~x)

xdata = c(1, 3, 5, 7, 9)
ydata = c(7, 33, 65, 110, 180)

logxdata = log(xdata)
logydata = log(ydata)

fitModel(logydata ~ A * logxdata + B)
## function (logxdata, ..., transformation = function (x) 
## x) 
## return(transformation(predict(model, newdata = data.frame(logxdata = logxdata), 
##     ...)))
## <environment: 0x7fcdf7a289d8>
## attr(,"coefficients")
##        A        B 
## 1.449432 1.915983 
## attr(,"class")
## [1] "nlsfunction" "function"

This tells us that \(A=1.45\) and \(B=1.92\). We solve for \(c\) and plot the function with the data

p = 1.45
p
## [1] 1.45
c = exp(1.92)
c
## [1] 6.820958
gf_point(ydata ~ xdata) %>%
  slice_plot(6.82 * x^1.45 ~ x, domain(x=1:9),  color='orange')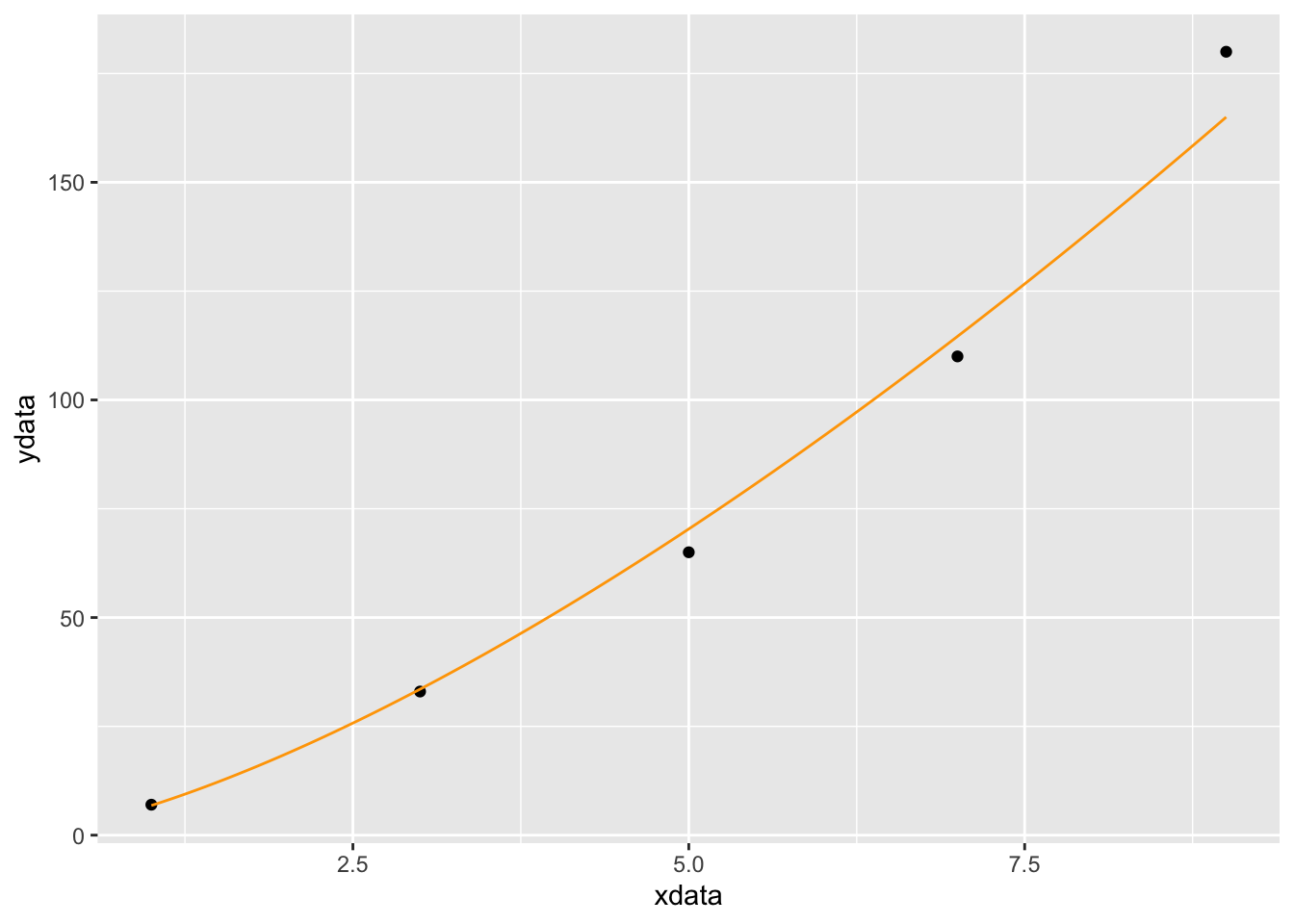

Fitting a Model by Specifying Starting Values

Sometimes fitModel fails to find a good model for the data. Here are two things that can happen.

  • The command fitModel fails, 7.complaining about a “singular gradient.” This means that fitModel picked a bad starting point, and can’t figure out how to improve it’s initial guess.
  • The command fitModel does find a function, but when we plot it, we realize that it’s not what we want.

Here is an example of fitModel returning a function that we don’t like. Let’s load in the `utilities.csv’ data set and look at the first few rows.

utilitydata = fetch::fetchData("utilities.csv")
## Retrieving from http://www.mosaic-web.org/go/datasets/utilities.csv
head(utilitydata)
##   month day year temp  kwh ccf thermsPerDay dur totalbill gasbill
## 1     2  24 2005   29  557 166          6.0  28    213.71  166.63
## 2     3  29 2005   31  772 179          5.5  33    239.85  117.05
## 3     1  27 2005   15  891 224          7.5  30    294.96  223.92
## 4    11  23 2004   43  860  82          2.8  29    160.26   88.51
## 5    12  28 2004   23 1160 208          6.0  35    317.47  224.18
## 6     9  26 2004   71  922  15          0.5  32    117.46   21.25
##   elecbill notes
## 1    47.08      
## 2    62.80      
## 3    71.04      
## 4    71.75      
## 5    93.29      
## 6    96.21

Now let’s plot temperature versus month

gf_point(temp ~ month, data=utilitydata)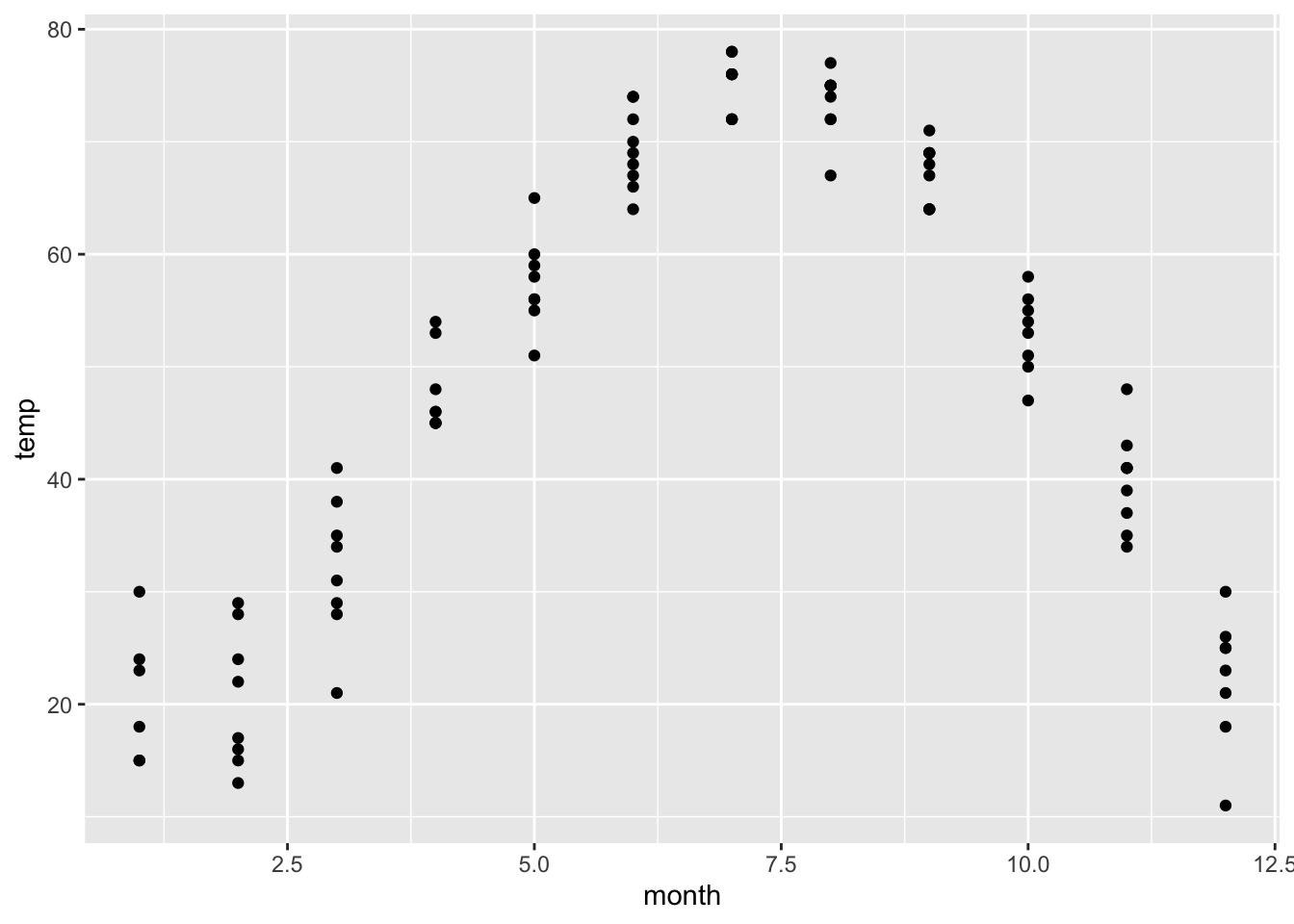

We have plotted monthly temperature data for multiple years. Let’s try to fit a periodic function.

M = fitModel(temp ~ A * sin(w*(month + p))+C, data=utilitydata)
coef(M)
##         A         w         p         C 
## -28.67993  -6.78753  56.15894  47.20908
f = makeFun(-28.7 * sin(-6.8*(t + 56.2))+47.2 ~ t)
gf_point(temp ~ month, data=utilitydata) %>%
  slice_plot(f(t)~t, domain(t=0:13), color='red')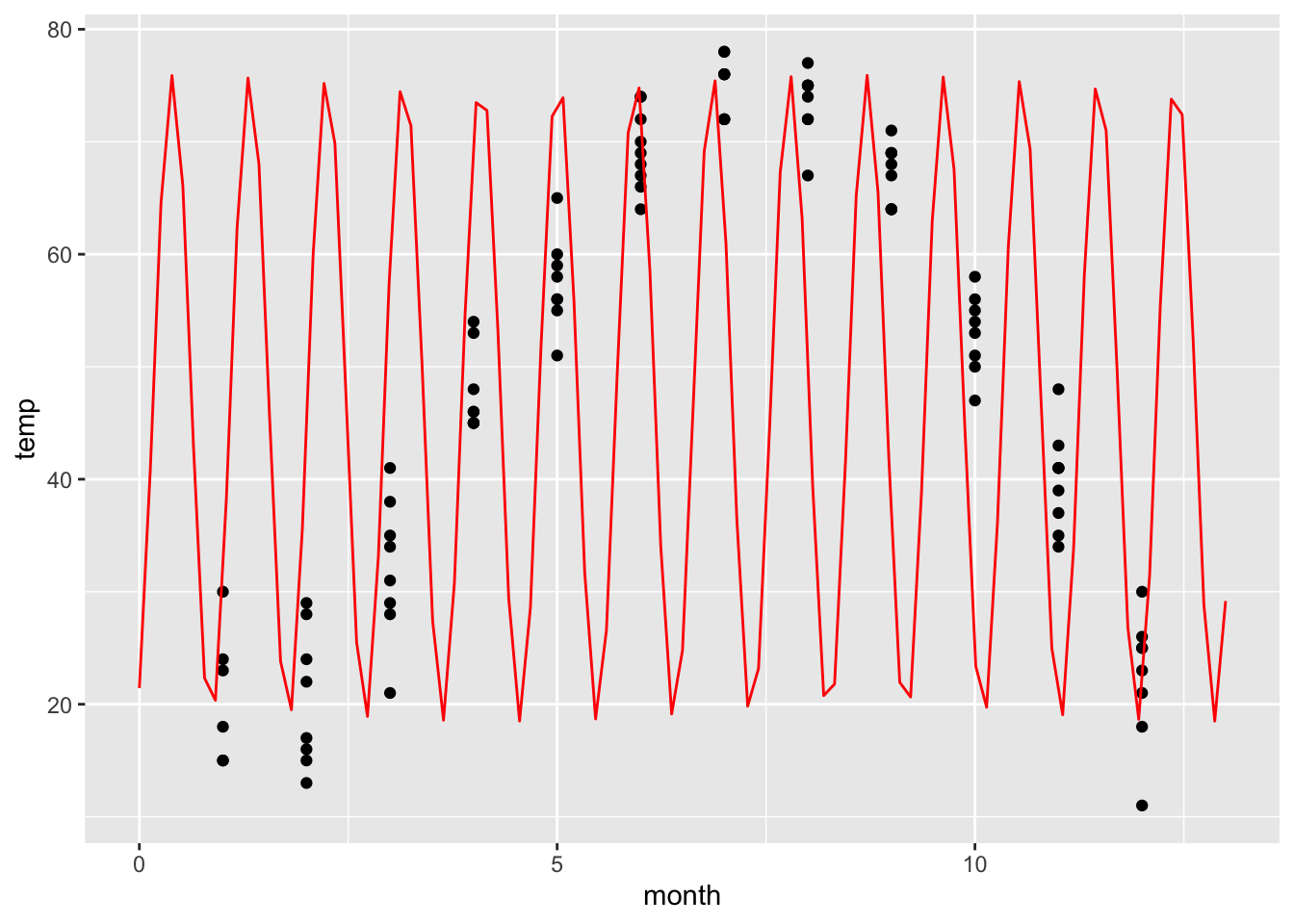

This is not what we wanted! It looks like fitModel was confused by the multiple data points for each month. So the frequency w is completely wrong. We can correct this by specifying an initial guess for w. We think that the period should be 12 months, so we want to start with w=2*pi/12.

M = fitModel(temp ~ A * sin(w*(month + p))+C, data=utilitydata, start=list(w=2*pi/12))
coef(M)
##           w           A           p           C 
##   0.5043435 -28.6799747 -22.8387987  47.2090049
f = makeFun(-28.7 * sin(0.5*(t -22.8))+47.2 ~ t)
gf_point(temp ~ month, data=utilitydata) %>%
  slice_plot(f(t)~t, domain(t=0:13), color='red')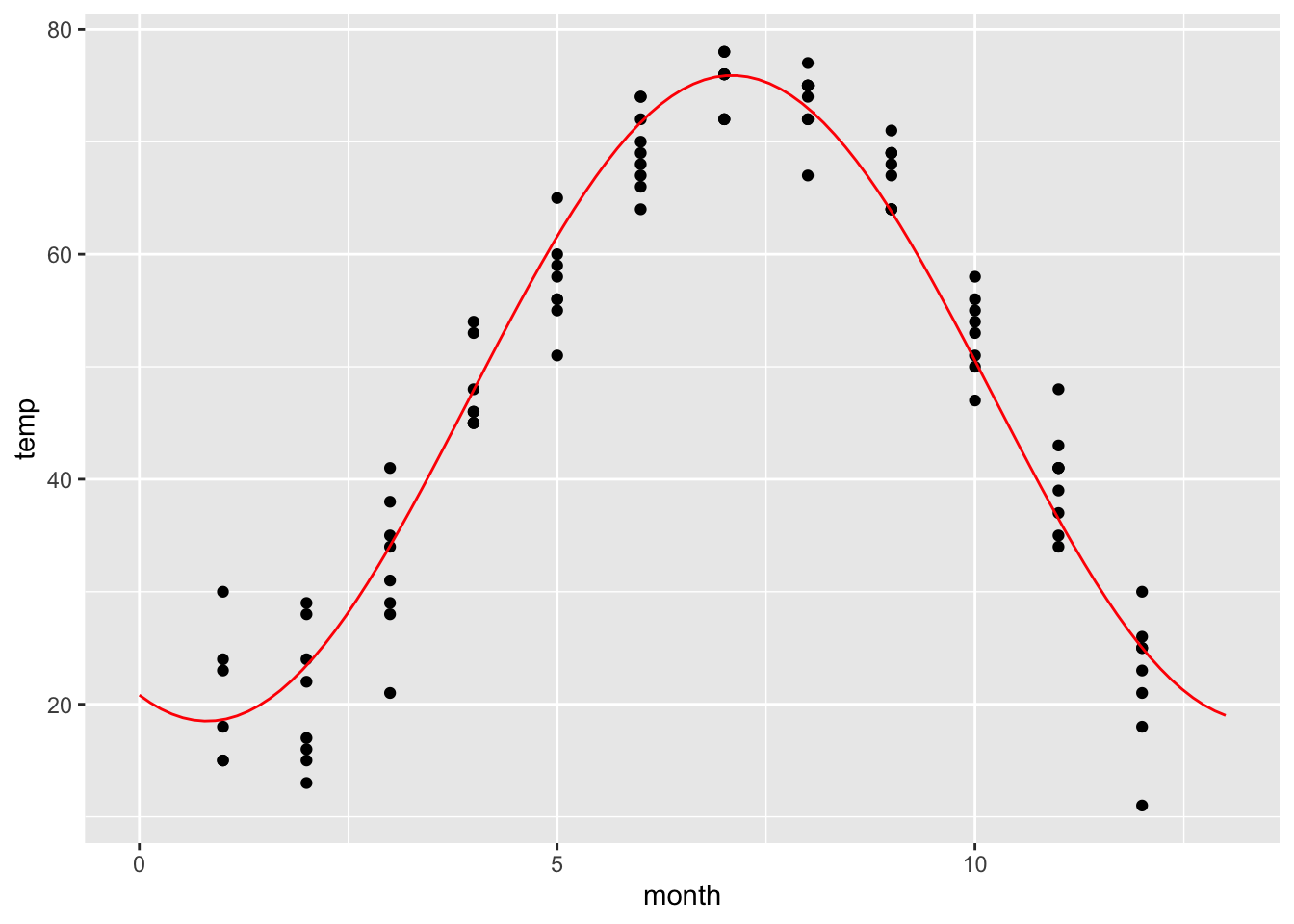

That looks much better!

Plotting Surfaces in 3D

We plot functions \(z = f(x,y)\) using the contour_plot command. We specify the independent variables with the syntax ~ x&y.

f = makeFun(x^2 - y^2 ~ x&y)

contour_plot(f(x,y) ~ x&y, domain(x=-2:2, y=-2:2))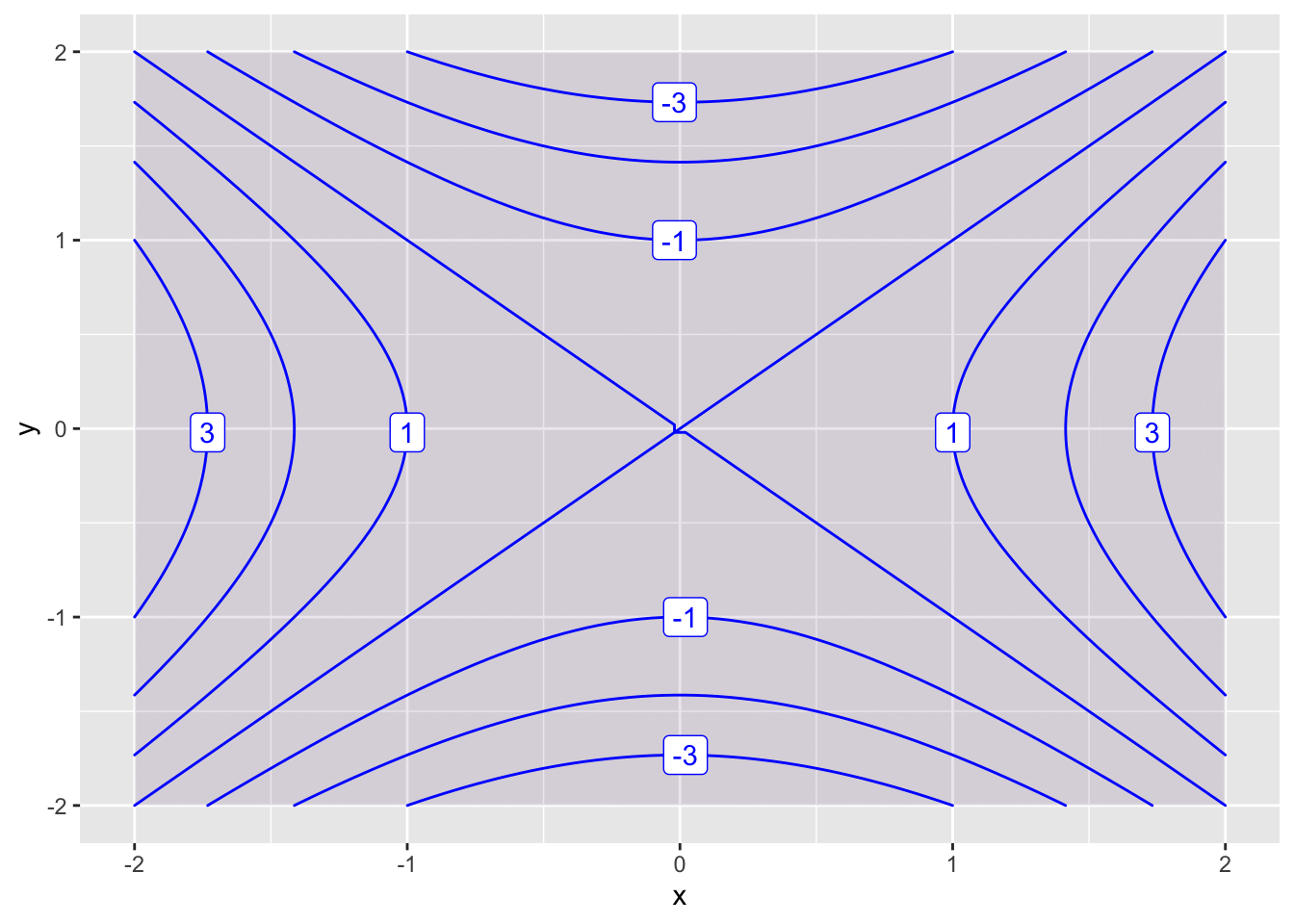

By default, RStudio labels every other countour. We can change this using the skip parameter. The default value of skip is 1. If we want to label every contour, we set skip=0.

f = makeFun(x^2 - y^2 ~ x&y)

contour_plot(f(x,y) ~ x&y, domain(x=-2:2, y=-2:2), skip=0)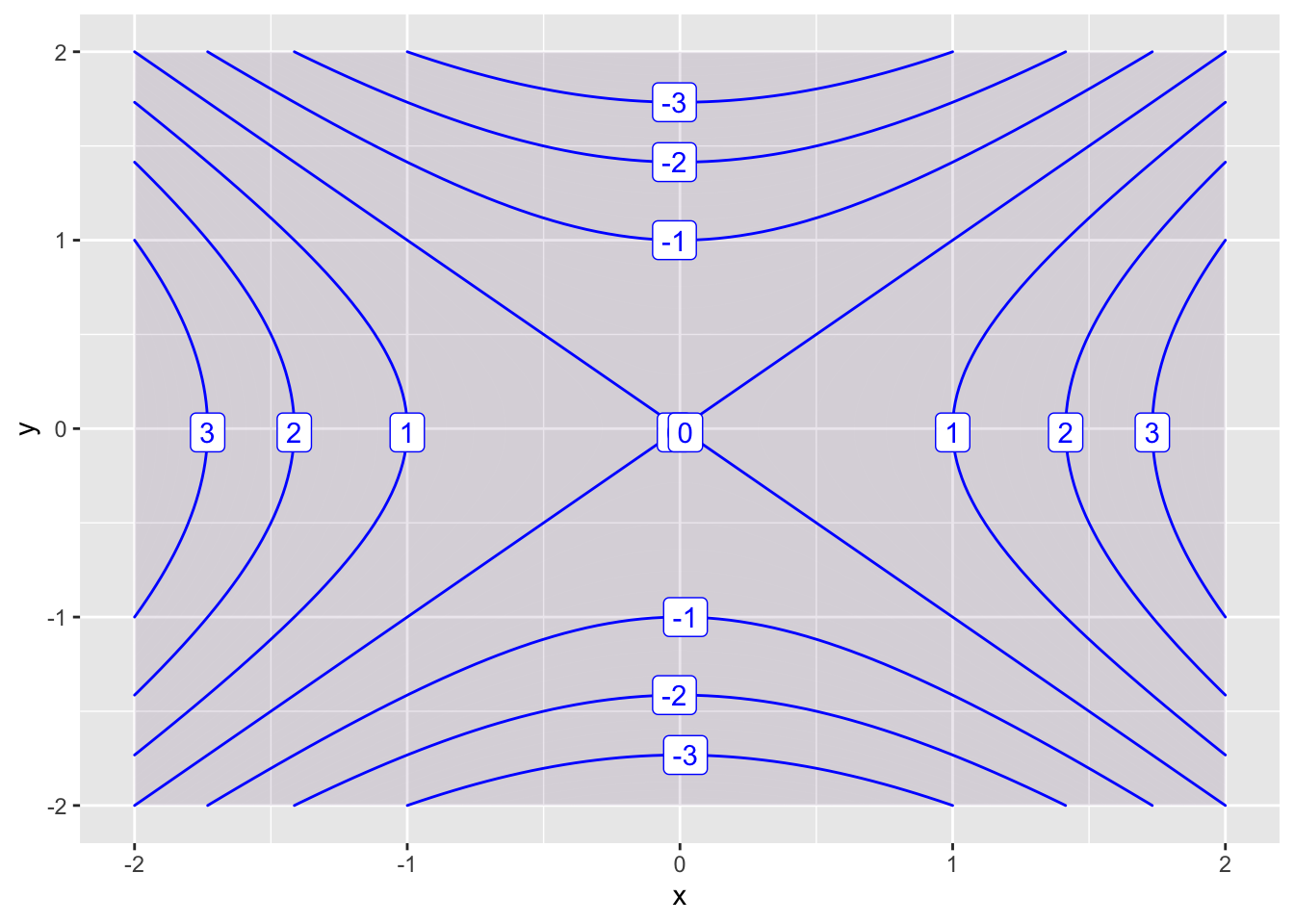

You can add more contours using the levels parameter, and turn off the shading with the filled parameter.

contour_plot(f(x,y) ~ x&y, domain(x=-2:2, y=-2:2), contours_at = seq(-3 ,3, .5))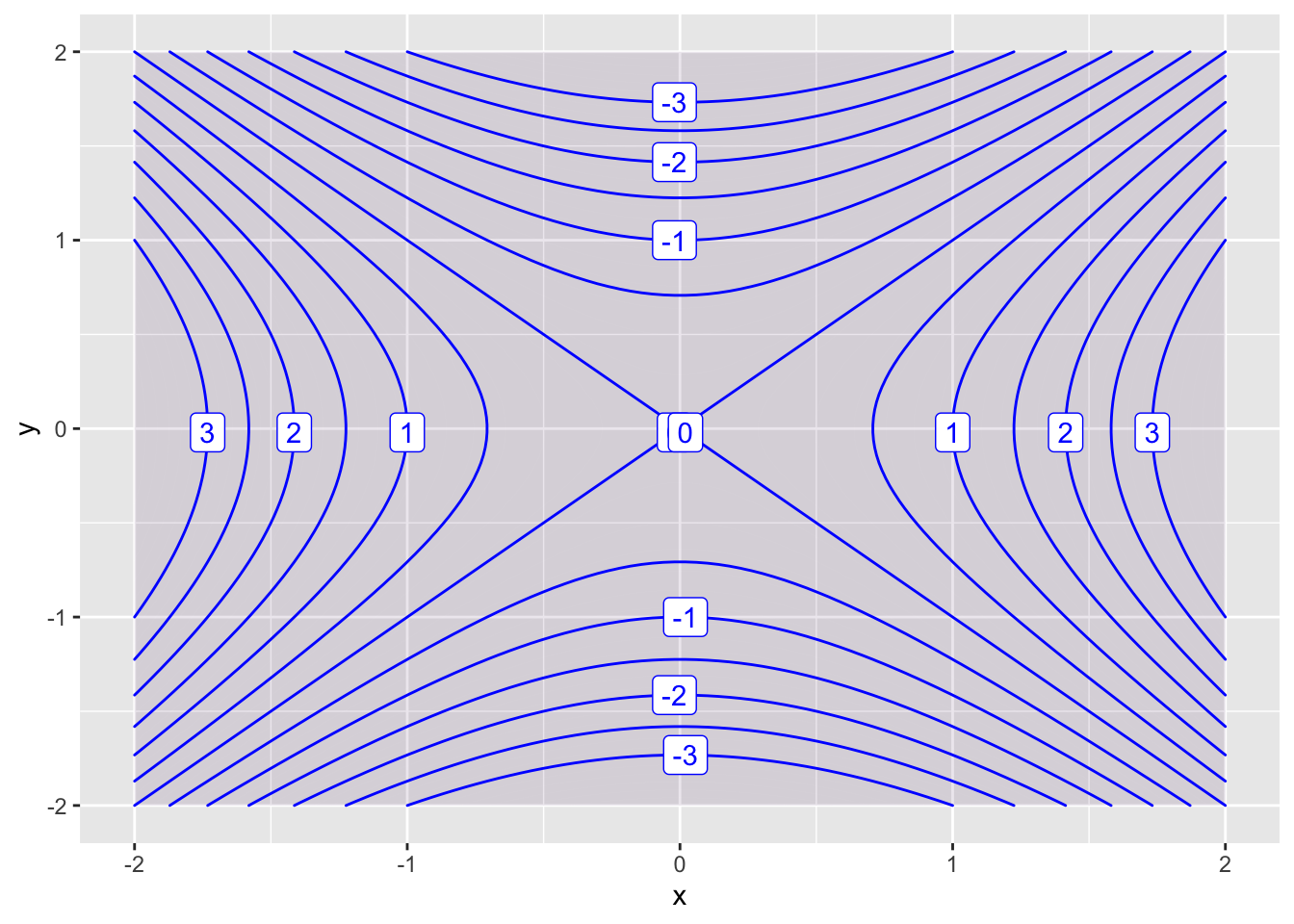

You can change the plot range using domain.

contour_plot(f(x,y) ~ x&y, domain(x=-20:20, y=-20:20))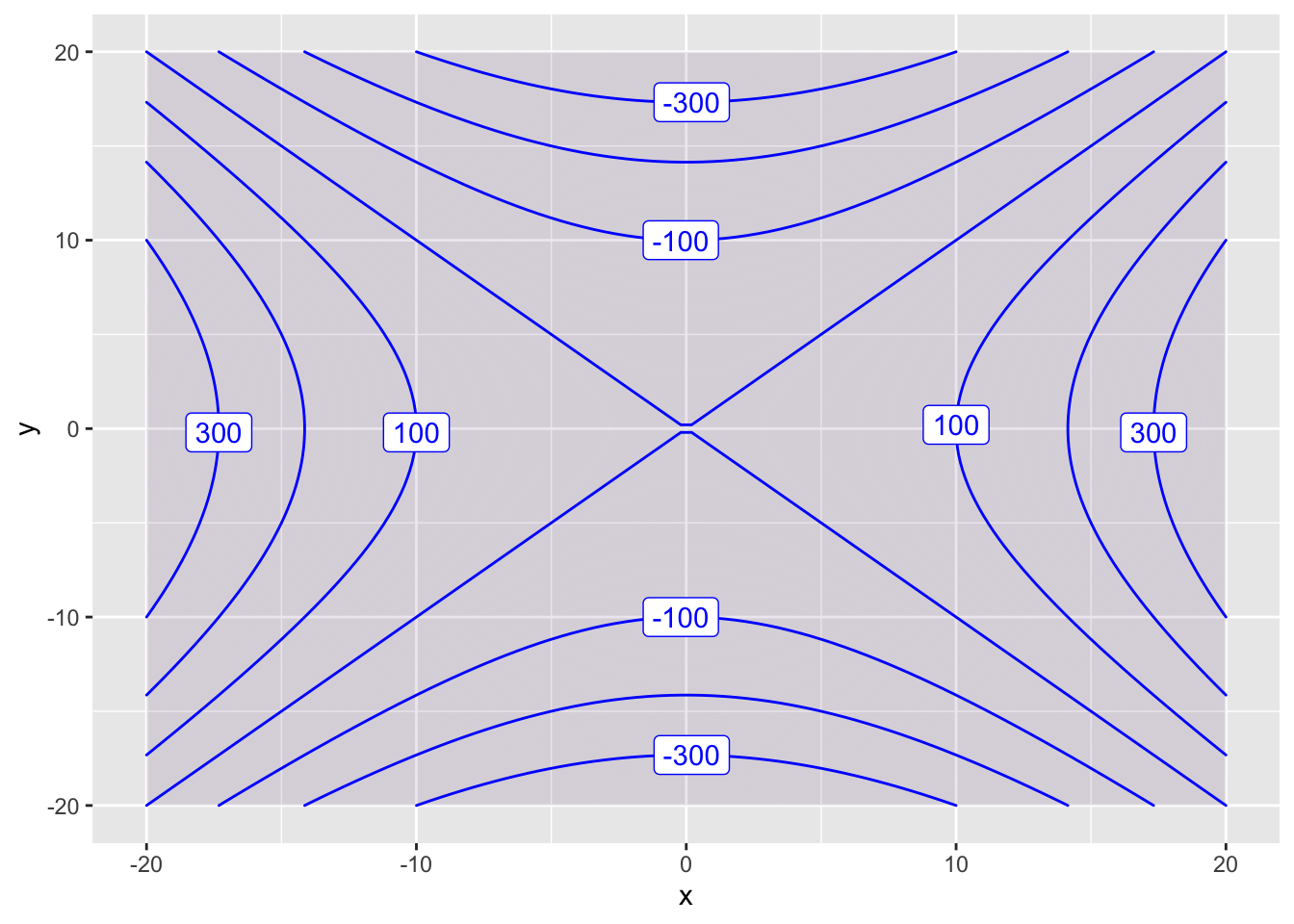

You can create a 3D plot interactive_plot.

interactive_plot(f(x,y) ~ x&y, domain(x=-20:20, y=-20:20))

Differentiation

Estimating the Derivative

We can estimate the derivative of \(f'(x)\) by using the average rate of change \[ f'(x) \approx\frac{f(x+\alpha)-f(x)}{\alpha} \] for some small number \(\alpha > 0\). Smaller and smaller \(\alpha\)’s lead to better and better approximations.

So we can estimate the derivative by using smaller and smaller \(\alpha\) values until our estimates stabilize. Here is an example that estimates \(f'(4)\) for the function \(f(x) = x^2 + 10*\sin(x)\).

f=makeFun(x^2+10*sin(x)~x)
alpha=c(1, 0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001, 0.0000001)
d=(f(4+alpha)-f(4))/alpha
d
## [1] 6.978782 1.952538 1.511513 1.468349 1.464042 1.463612 1.463569
## [8] 1.463564

The estimates stabilize to the value \(1.46356\). So our estimate is \(f'(4) \approx 1.46456\)

Estimating the Partial Derivative

We can use the same method to estimate the partial derivates of \(g(x,y)\). We have \[ \frac{\partial g}{\partial x} \approx\frac{g(x+\alpha,y)-f(x,y)}{\alpha} \quad \mbox{and} \quad \frac{\partial g}{\partial y} \approx\frac{g(x,y+\alpha)-f(x,y)}{\alpha} \] Let’s estimate the partial derivatives of \(g(x,y) = e^{x \sin(y)}\) at the point \((2, 7)\). First, let’s estimate \(g_x(2,7) = \left. \frac{\partial g}{\partial x} \right|_{(2,7)}\). The code is very similar to the code we used for a single variable function.

g=makeFun(exp(x*sin(y))~x&y)
alpha=c(1, 0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001, 0.0000001)
d=(g(2+alpha,7)-g(2,7))/alpha
d
## [1] 3.456634 2.526691 2.452648 2.445403 2.444680 2.444608 2.444601
## [8] 2.444600

We conclude that \(g_x(2,7) \approx 2.445.\)

Now let’s estimate \(g_y(2,7) = \left. \frac{\partial g}{\partial y} \right|_{(2,7)}\). All we need to do is move alpha into the \(y\)-variable.

g=makeFun(exp(x*sin(y))~x&y)
alpha=c(1, 0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001, 0.0000001)
d=(g(2,7+alpha)-g(2,7))/alpha
d
## [1] 3.512524 5.761618 5.628032 5.612215 5.610611 5.610450 5.610434
## [8] 5.610433

We conclude that \(g_y(2,7) \approx 5.610.\)

Constrained Optimization

Suppose that we want to find the maximum of the production function \(P(x,y)=3000x^{0.2}y^{0.8}\) given the constraint \(Q(x,y)= 4x + 3y = 200\).

We want to make a contour plot of \(P(x,y)\) and then add the constraint. The maximum value is achieved where the constraint \(Q(x,y)=300\) is tangent to the contour curve of \(P(x,y)\).

P = makeFun( x^(0.2) * y^(0.8) ~ x&y)
Q = makeFun( 4*x + 3*y ~ x&y)

contour_plot(P(x,y)~x&y, domain(x=0:80, y=0:80), 
             contours_at=seq(20,80,5), skip=0) |>
  contour_plot(Q(x,y) ~ x & y, contour_color="black", 
               contours_at=c(200), label_placement=.25)
## Scale for 'colour' is already present. Adding another scale for
## 'colour', which will replace the existing scale.
## Scale for 'fill' is already present. Adding another scale for
## 'fill', which will replace the existing scale.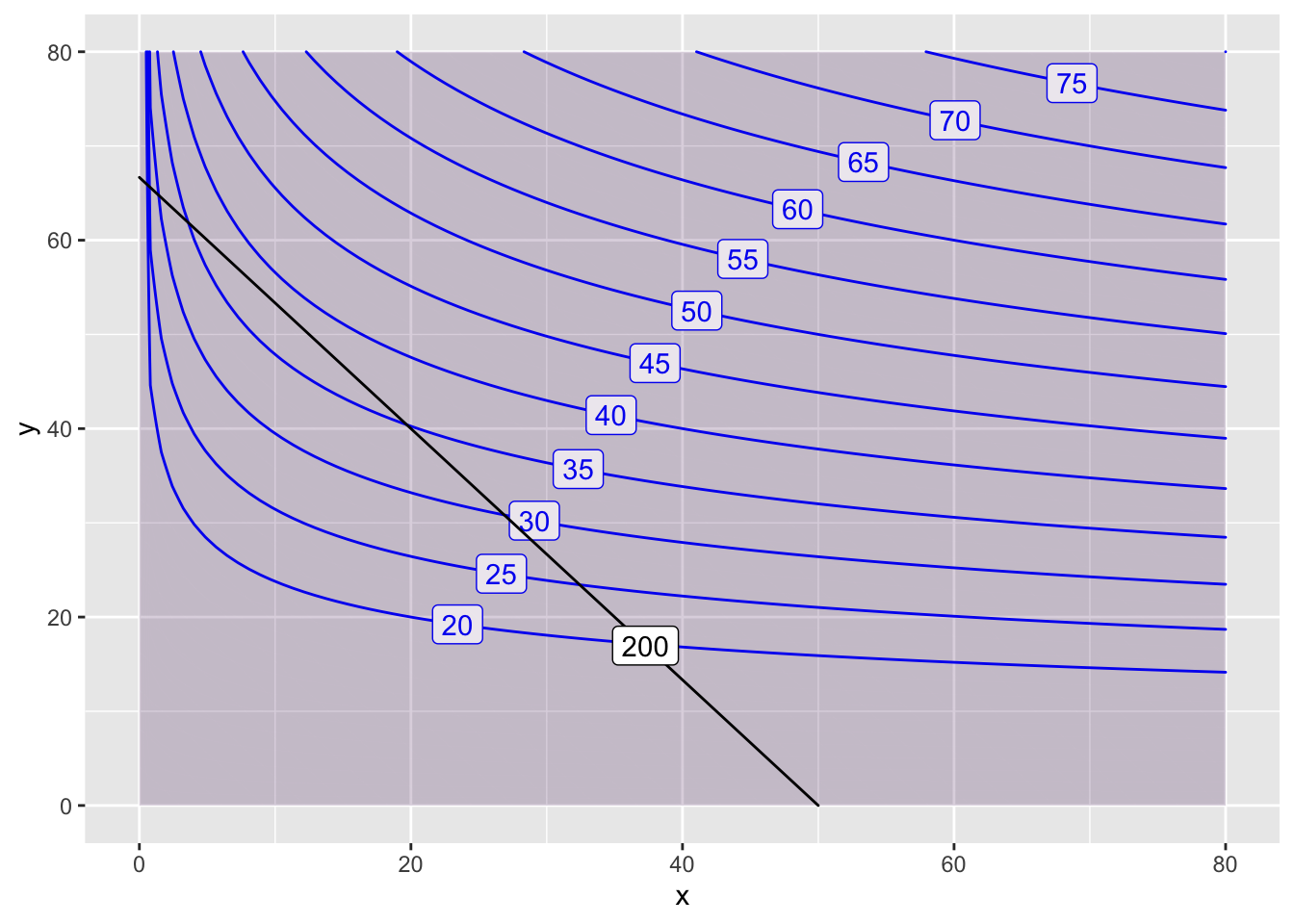

In this case, the optimal value of \(38\) is achieved at approximately \((10, 55)\). Let’s make another plot to get a better estimate.

contour_plot(P(x,y)~x&y, domain(x=0:40, y=20:60), 
             contours_at=seq(20,50,2), skip=0) |>
  contour_plot(Q(x,y) ~ x & y, contour_color="black", 
               contours_at=c(200), label_placement=.25)
## Scale for 'colour' is already present. Adding another scale for
## 'colour', which will replace the existing scale.
## Scale for 'fill' is already present. Adding another scale for
## 'fill', which will replace the existing scale.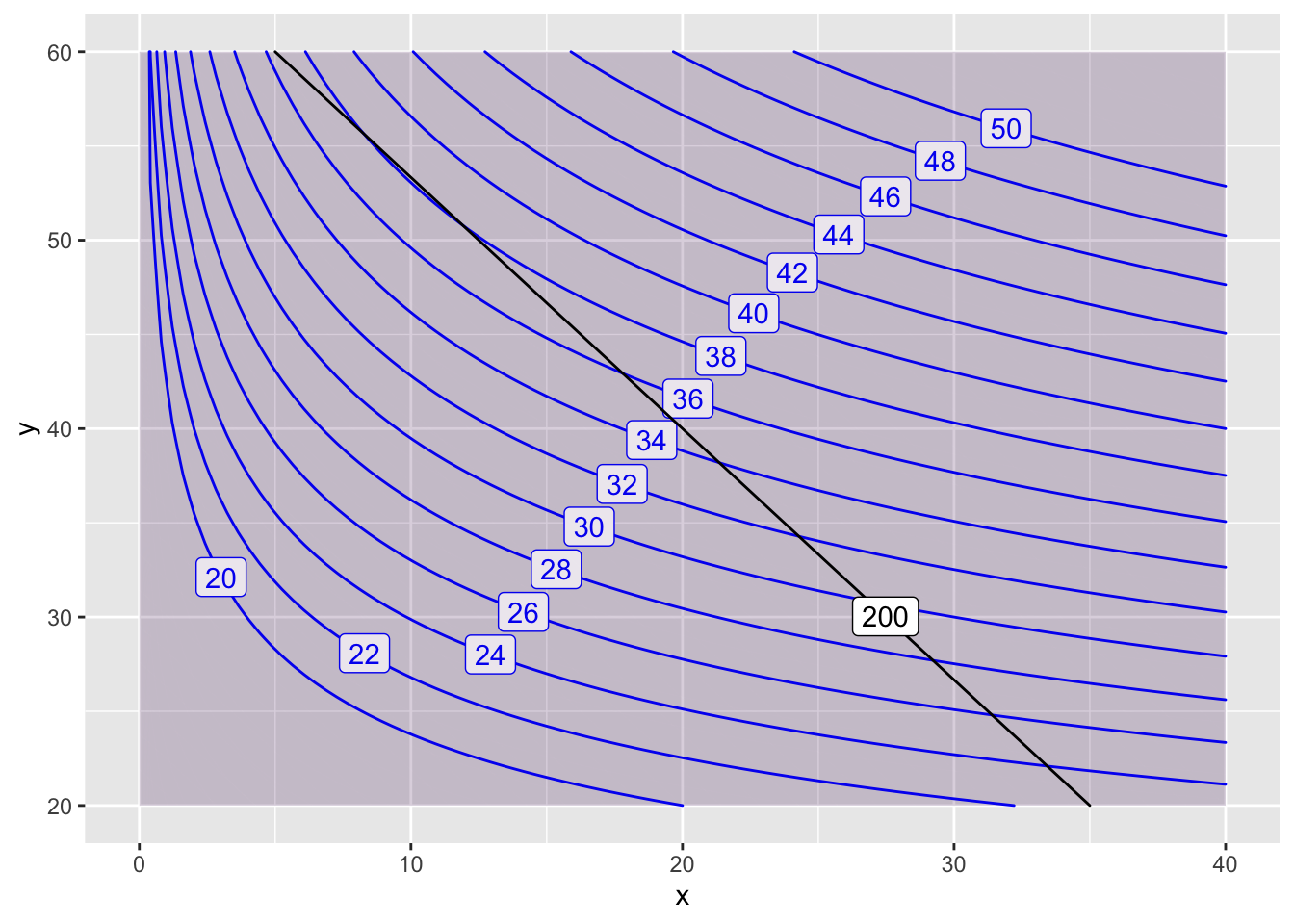

On this zoomed in plot, we can refine our estimate a bit. The maximum \(f(10,53)=38\) is achieved at \(x=10\) and \(y=53\).

Now, if I want to estimate the Lagrange multiplier \(\lambda\), I would change my constraint a little bit (say to \(210\)) and then look at the change in the optimal value.

contour_plot(P(x,y)~x&y, domain(x=0:40, y=20:60), 
             contours_at=seq(20,50,2), skip=0) |>
  contour_plot(Q(x,y) ~ x & y, contour_color="black", 
               contours_at=c(200,210), skip=0, 
               label_placement=.25)
## Scale for 'colour' is already present. Adding another scale for
## 'colour', which will replace the existing scale.
## Scale for 'fill' is already present. Adding another scale for
## 'fill', which will replace the existing scale.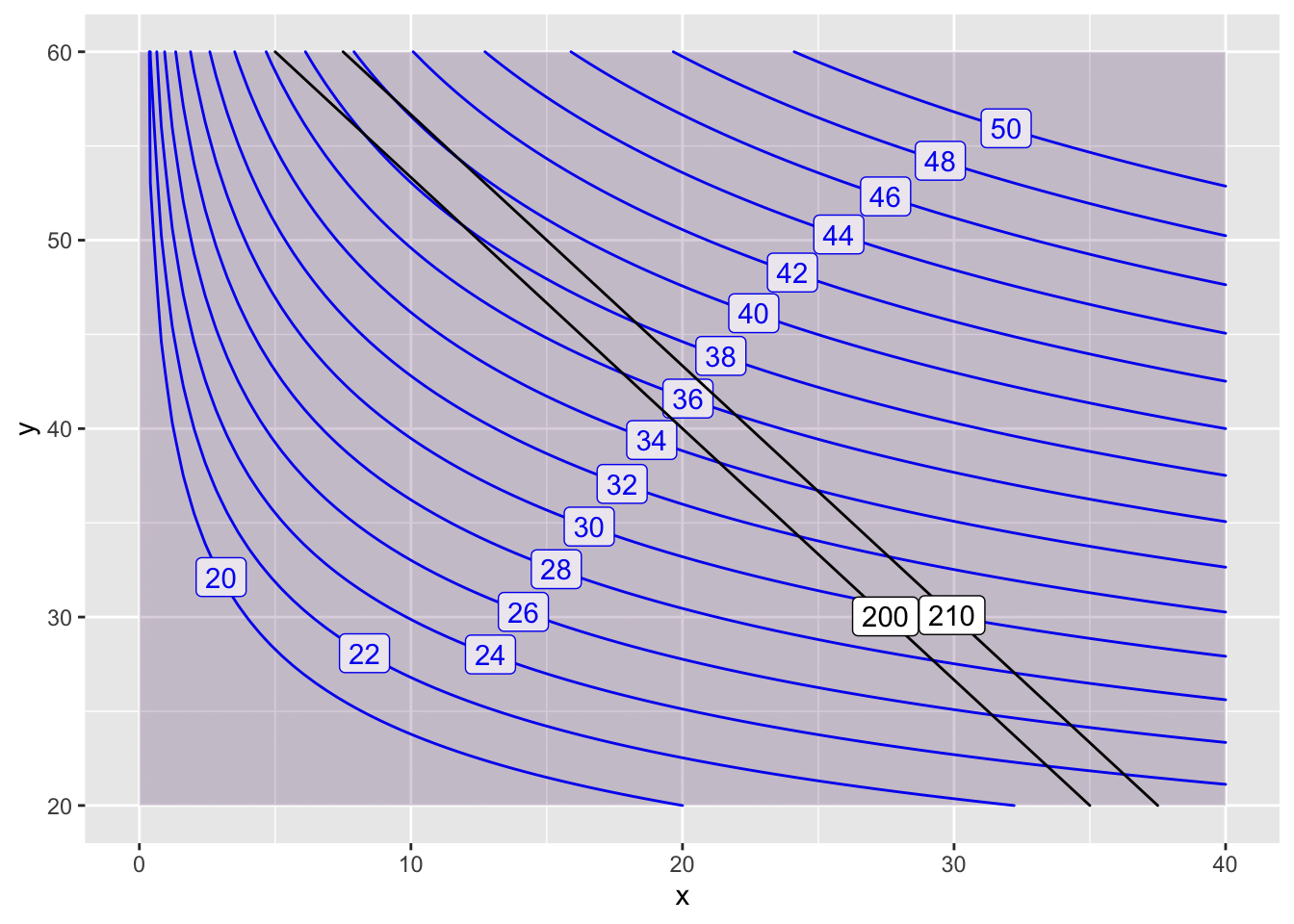

We have \[ \lambda = \frac{\triangle \mbox{optimal value}}{\triangle \mbox{constraint}} = \frac{40 - 38}{210-200} = \frac{2}{10} = 0.2. \]

Integration

Estimating the Definite Integral

The define integral \(\int_{a}^b f(x) dx\) is the signed area between the curve \(y=f(x)\) and the \(x\)-axis. We approximate this area by partitioning the interval \([a,b]\) into smaller intervals of width \(\triangle x\) and then summing the areas \(f(x) \triangle x\) of the corresponding rectangles.

Here is code that makes this approximation for the function \(f(x) = x + \sin(x^2)\) over the interval \([5,10]\). The code splits this interval into 100 subintervals. You can get a better approximation by increasing the denominator of base=(b-a)/100 to a much larger number, for example: base=(b-a)/1000000.

f=makeFun(x + sin(x^2)~x)
a=5
b=10
base=(b-a)/100
points=seq(from=a+base, to=b, by=base)
heights=f(points)
areas=base*heights
sum(areas)
## [1] 37.67298

Differential Equations

Euler’s Method

Euler’s Method repeatedly uses Local Linear Approximation to find an approximate solution to a differential equation. Here is code that uses Euler’s Method to find an approximate solution for the following problem:

  • Differential equation \(\displaystyle{\frac{dx}{dt} = 3x - x^2}\)
  • Initial point \(t_0=2\) and \(x_0= 5\)
  • End time \(T=9\)
  • Step size \(\triangle t = 0.01\)
# derivative, initial conditions and setup
dxdt = makeFun(3*x - x^2 ~ x)
tstart = 2
xstart = 5
tend = 9
dt = 0.01
num = (tend - tstart)/dt
# Euler's Method code
t = tstart
x = xstart
tlist = t
xlist = x
for (i in 1:num) {
  x = x + dt * dxdt(x)
  t = t + dt
  tlist = c(tlist, t)
  xlist = c(xlist, x)
}
# print the ending point
c(tail(tlist,1),  tail(xlist,1))
## [1] 9 3
# plot the approximate function
gf_point(xlist ~ tlist)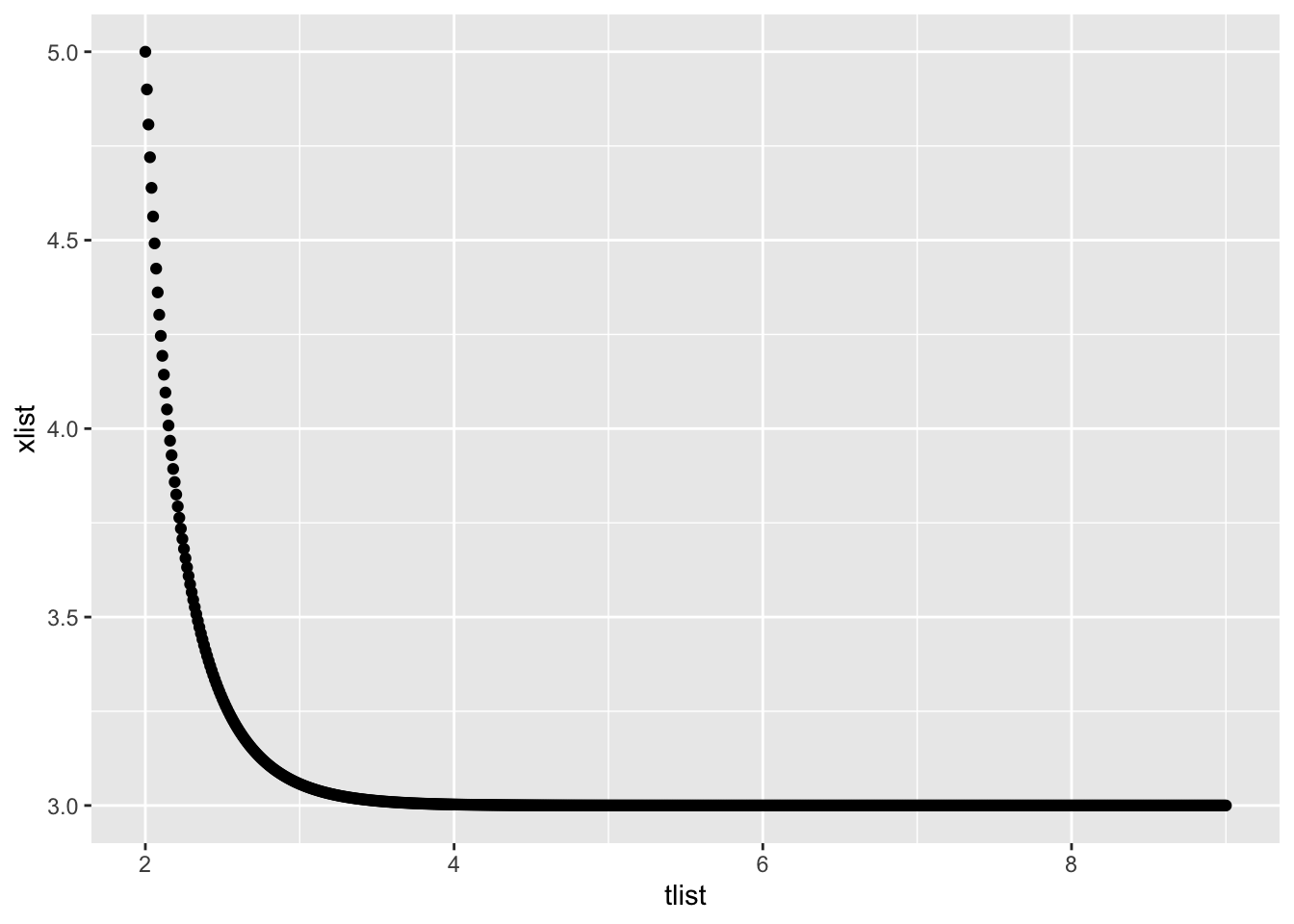

Slope Fields

The mosaicCalc package has a vectorfield_plot function that we use to create a slope field. So we need to make sure that this package has been loaded into RStudio.

suppressPackageStartupMessages(library(mosaicCalc))

Here is the code to create the slope field for \(\displaystyle{\frac{dP}{dt} = 5 - 2 P}\)

vectorfield_plot(t ~ 1,
P ~ 6 - 2 * P,
domain(t=-8:8, P=-8:8))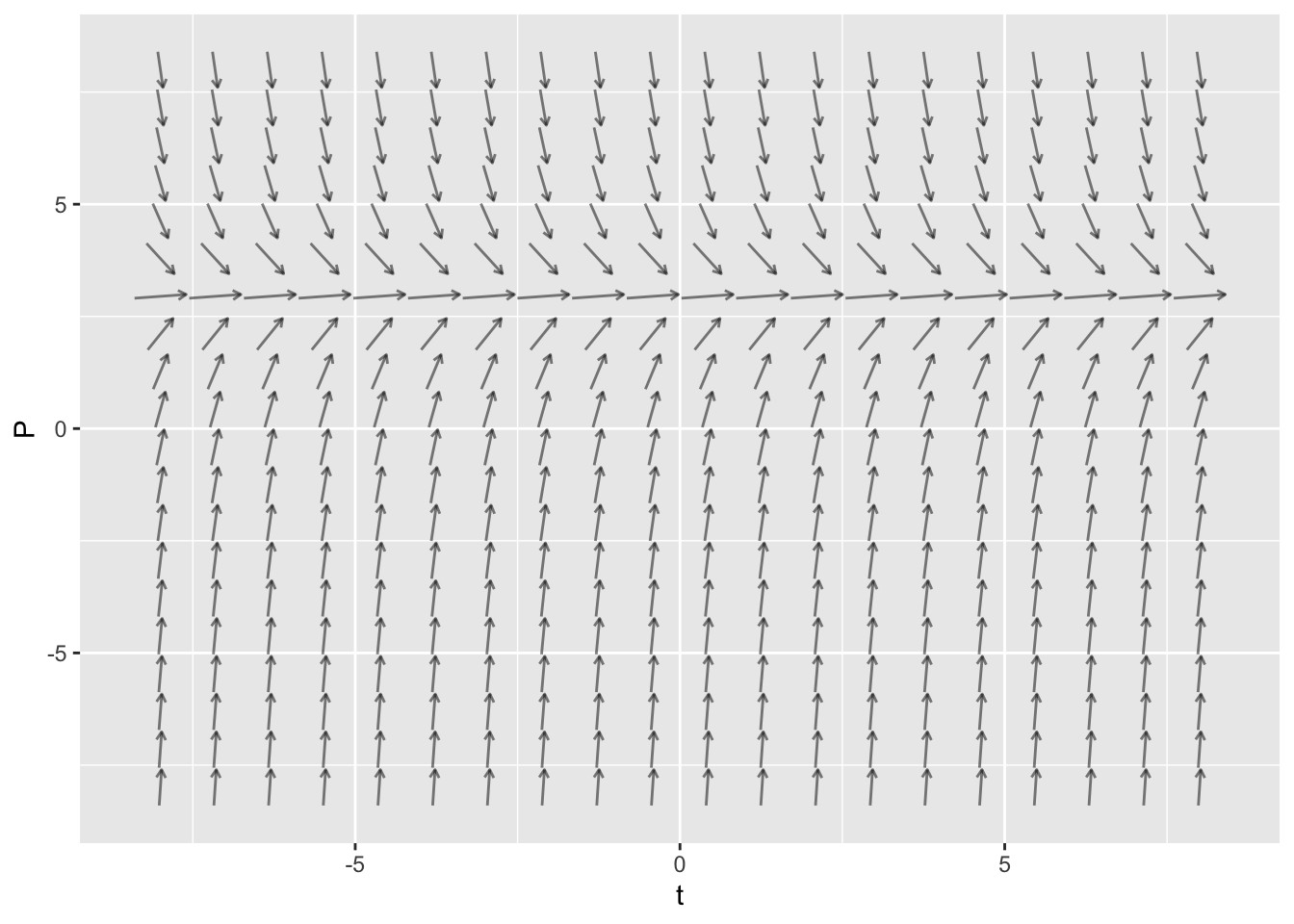

Creating a Trajectory in RStudio

The mosaicCalc package also has a traj_plot function that plots a solution curve to a differential equation through a given initial point.

Here is the code to plot the trajectory starting at \(P(0)=6\) for the differential equation \(\displaystyle{\frac{dP}{dt} = 6 - 2 P}\). In the code below, the nt parameter indicated the number of “tick marks” to use along the trajectory.

dyn = makeODE( dP ~  6 - 2 * P )
soln = integrateODE(dyn, domain(t=0:5), P=6)
traj_plot(P(t) ~ t, soln,  nt=5)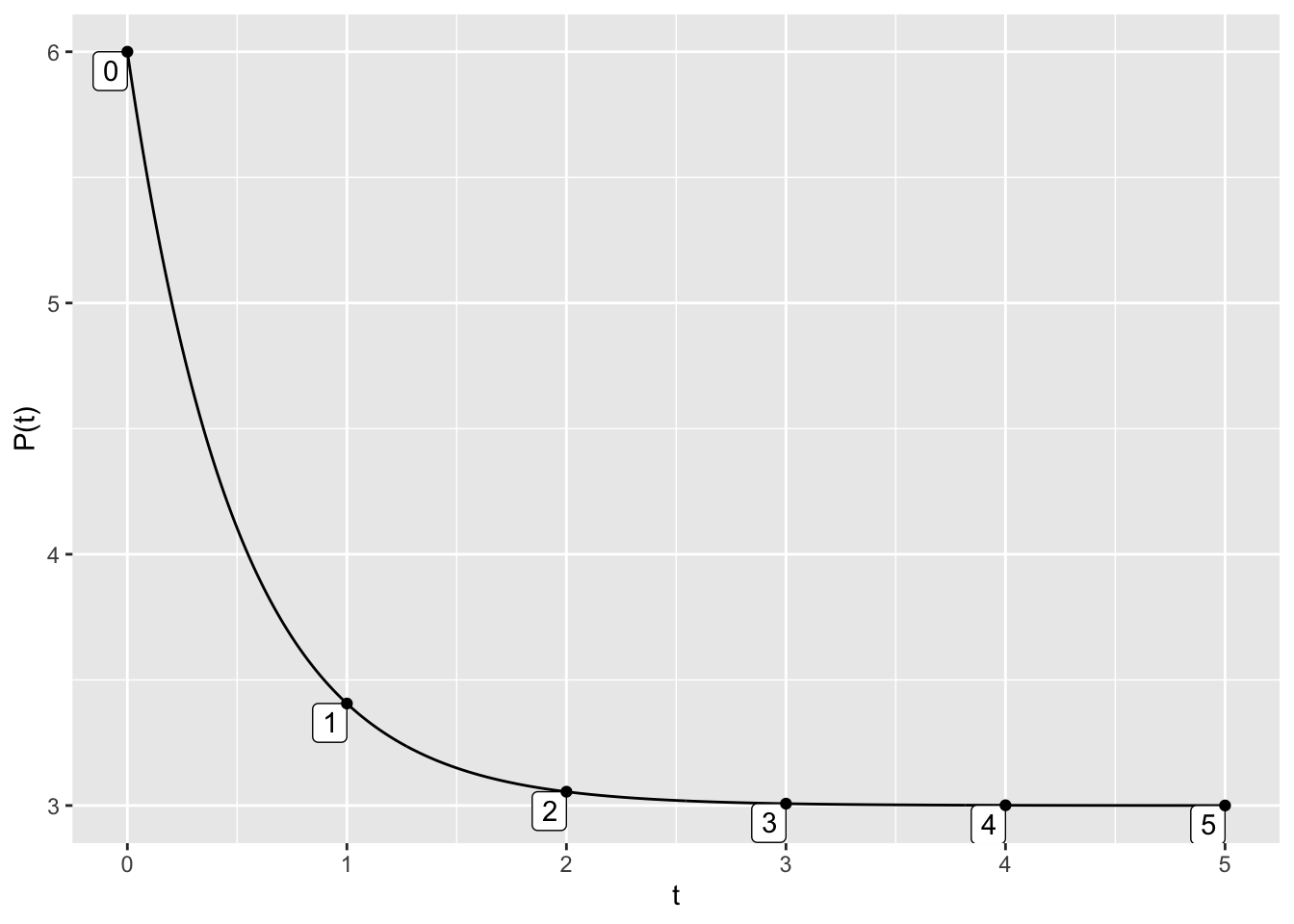

In fact, we can get fancier by making a single plot that has two trajectories (one for \(P(0)=6\) and one for \(P(0)=2\)) along with the vector field.

dyn = makeODE( dP ~  6 - 2 * P )
soln1 = integrateODE(dyn, domain(t=0:5), P=6)
soln2 = integrateODE(dyn, domain(t=0:5), P=2)
traj_plot(P(t) ~ t, soln1, color="blue", nt=5) %>%
  traj_plot(P(t) ~ t, soln2, color="magenta", nt=5) %>%
  vectorfield_plot(t ~ 1, P ~ 6 - 2 * P, domain(t=0:5, P=0:8))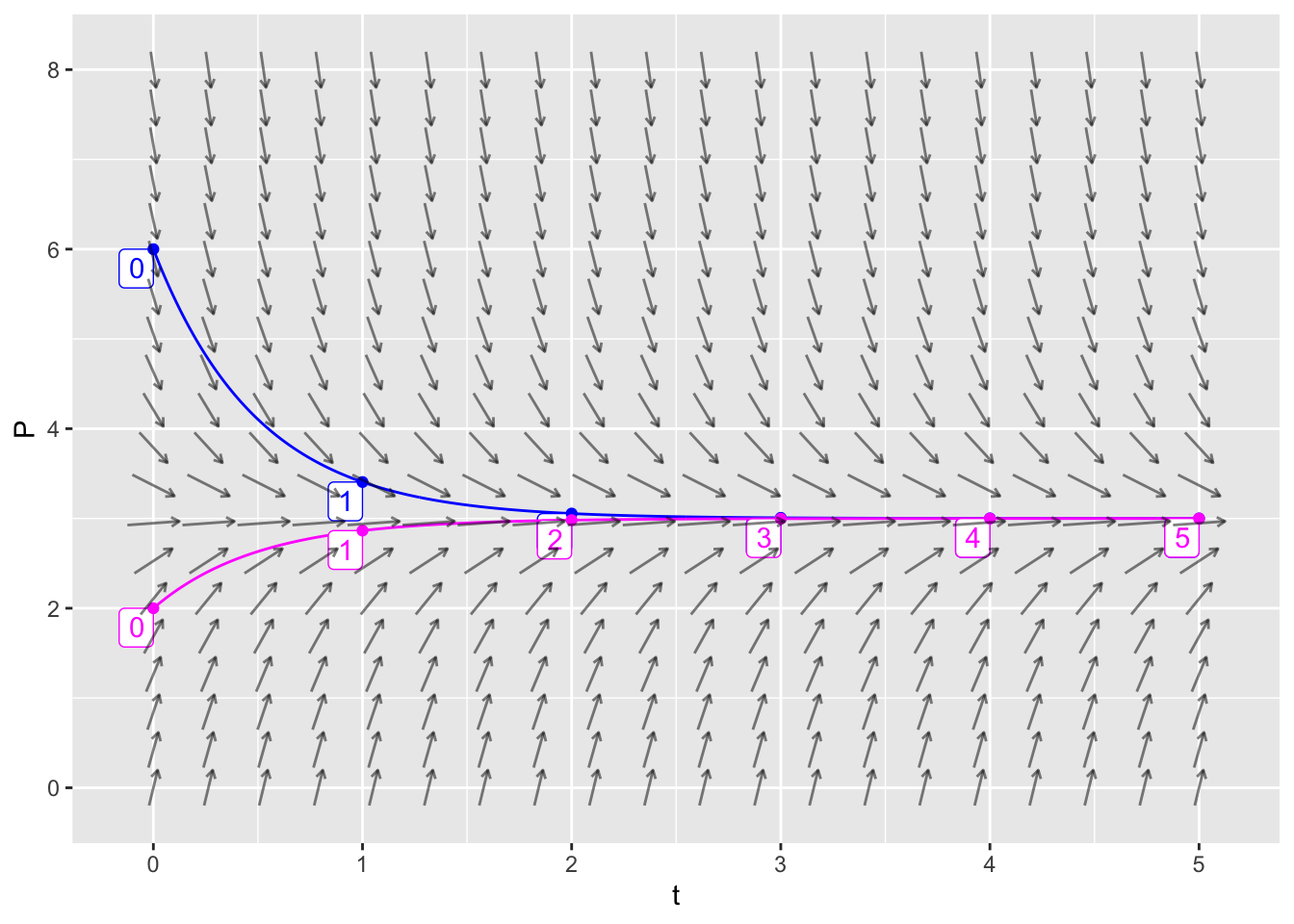

SIR Model

The mosaicCalc package has a vectorfield_plot function that we use to create a slope field, and a traj_plot function that we use to plot a trajectory. So we need to make sure that this package has been loaded into RStudio.

suppressPackageStartupMessages(library(mosaicCalc))

Here is some example code that plots an SIR slope field where

  • The infection rate is \(a=0.001\)
  • The removal rate is \(b=0.2\)
  • \(0 \leq S \leq 800\)
  • \(0 \leq I \leq 100\)

The horizontal axis is the susceptible population and the vertical axis is the infected population.

vectorfield_plot(S ~ - 0.001*S*I, 
                 I ~ 0.001*S*I -0.2*I, 
                 domain(S=0:800, I=0:100), 
                 transform=function(L) L^0.01)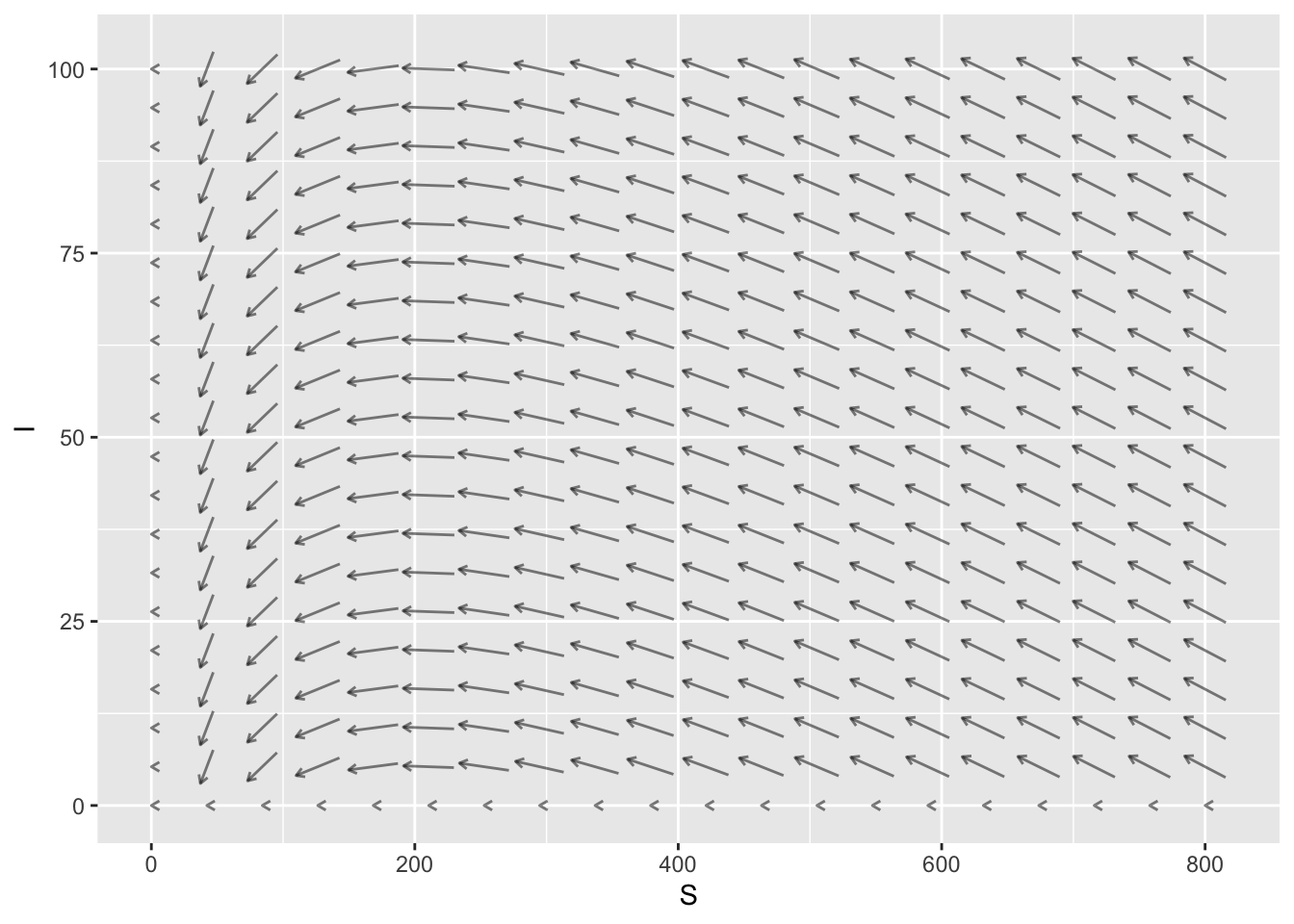

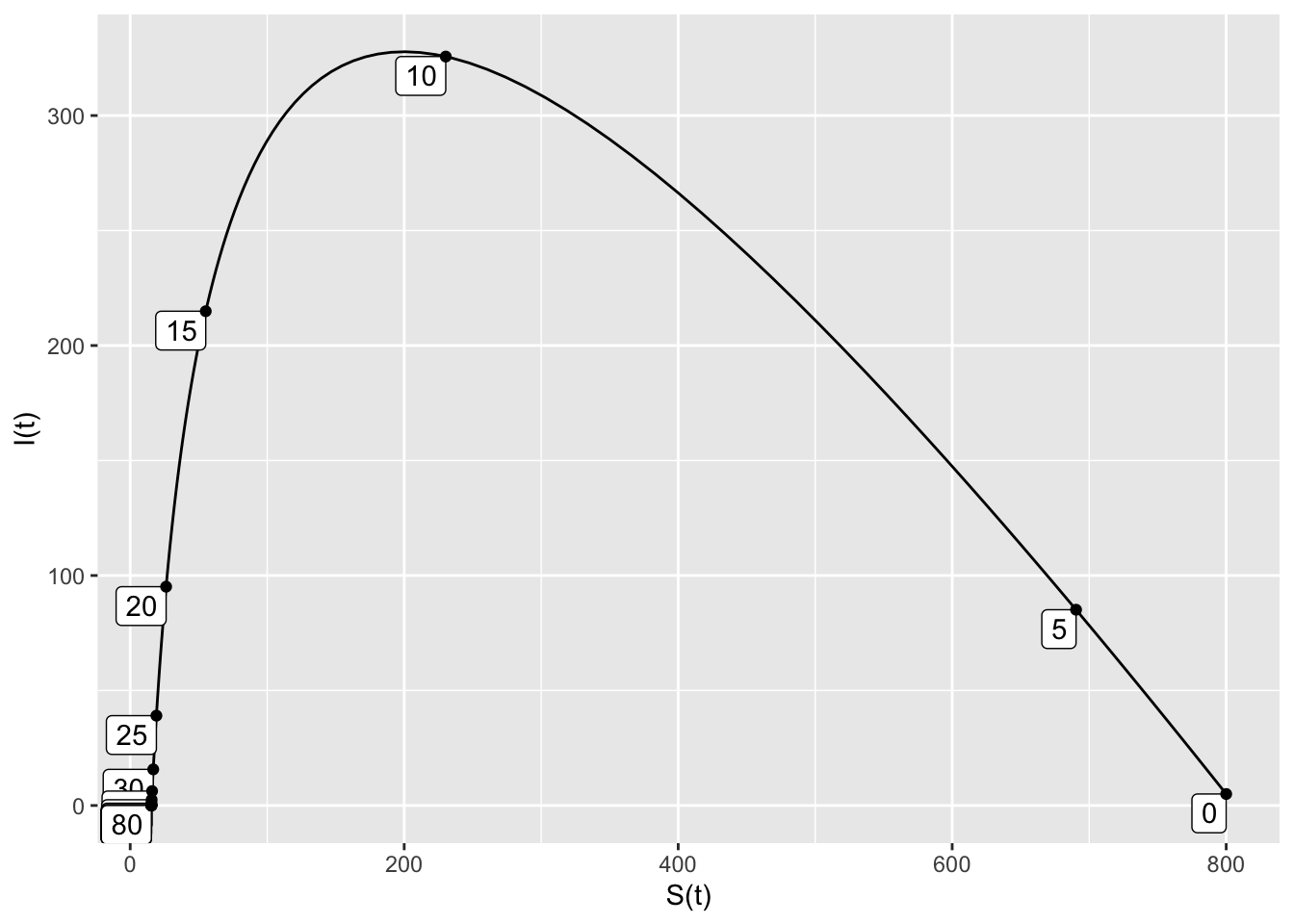
Here is some example code that plots a single SIR trajectory for this same model. Here are the additional inputs:

  • domain(t=0:80) means that the trajectory runs for \(0 \leq t \leq 80\).
  • S=800 means that the initial susceptible population is 800.
  • I=5 means that the initial infected population is 5.
  • nt=20 means that 20 tick marks will be added to the trajectory, showing the time that the point \((S,I)\) occurs.
SIRdyn = makeODE(dS ~ - 0.001*S*I, 
                  dI ~  0.001*S*I -0.2*I )
Soln = integrateODE(SIRdyn, domain(t=0:80), S=800, I=5)
traj_plot(I(t) ~ S(t), Soln, nt=20)
## Solution containing functions S(t), I(t).