6.B The Definite Integral
Introduction
Here is some code that approximates the area under \(f(x)=x^2\) on the interval \([a,b]\) using right hand endpoints on 100 subintervals. (How would you change this code to use left hand endpoints instead?)
f=makeFun(x^2 ~ x)
a = 0
b = 3
num = 100
### the approximation of f(x) on interval [a,b]
base = (b-a)/num
points = seq(from=a+base, to=b, by=base)
heights = f(points)
areas = base*heights
sum(areas)## [1] 9.13545Activities
Drive My Car
A car is driving at a rate of \(v(t)=-t+5\). Here is a plot of the velocity.
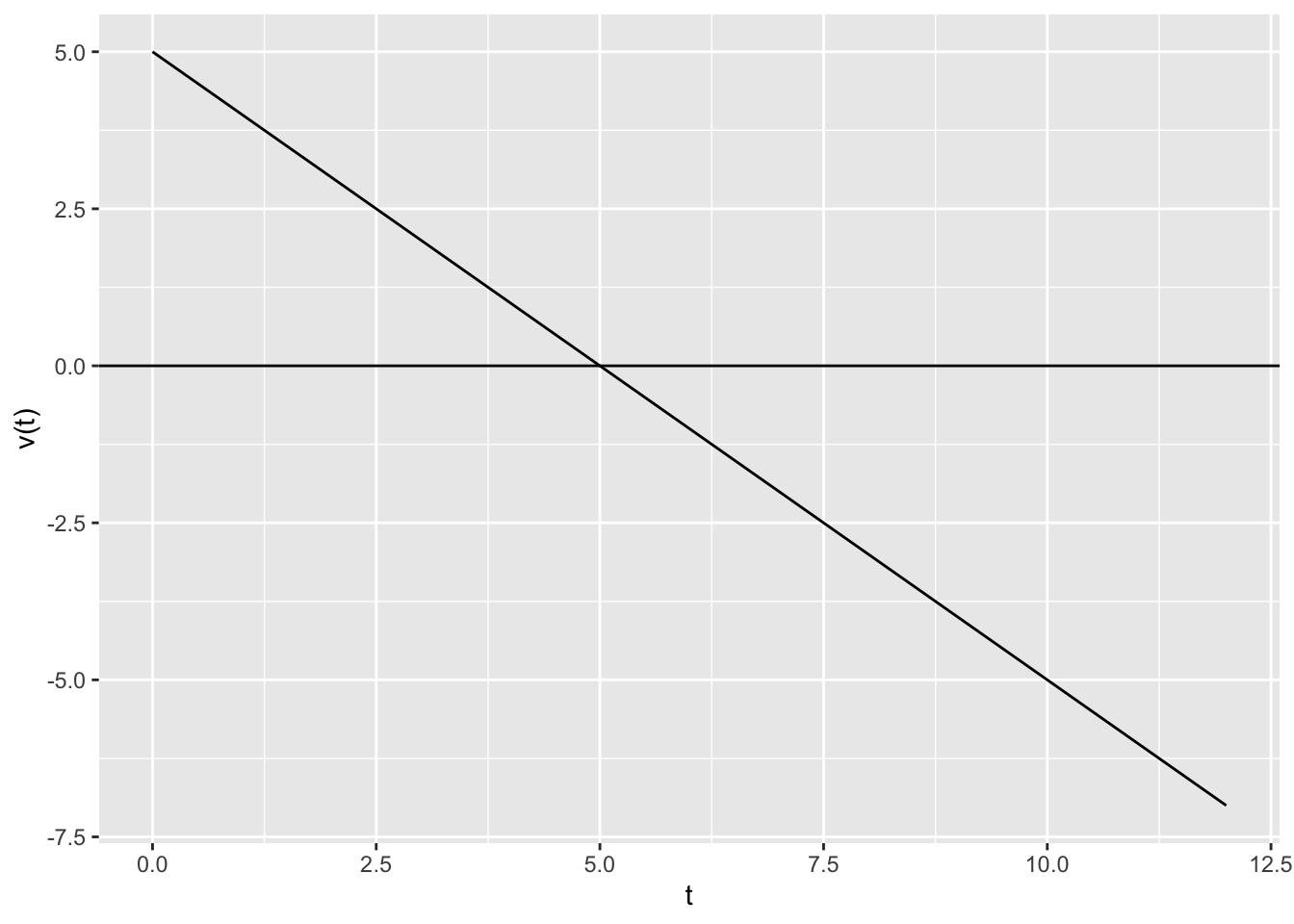
- Use RStudio to approximate these definite integrals using 1000 subintervals.
- \(\displaystyle{\int_0^5 v(x)dx}\)
- \(\displaystyle{\int_0^8 v(x)dx}\)
- \(\displaystyle{\int_0^{12} v(x)dx}\)
When does the car turn around?
When does the car return to where it started?
Accelerate My Car
A car is traveling at 55 feet per second at time \(t=0\). The plot below shows the car’s acceleration on the interval \([0,18]\).
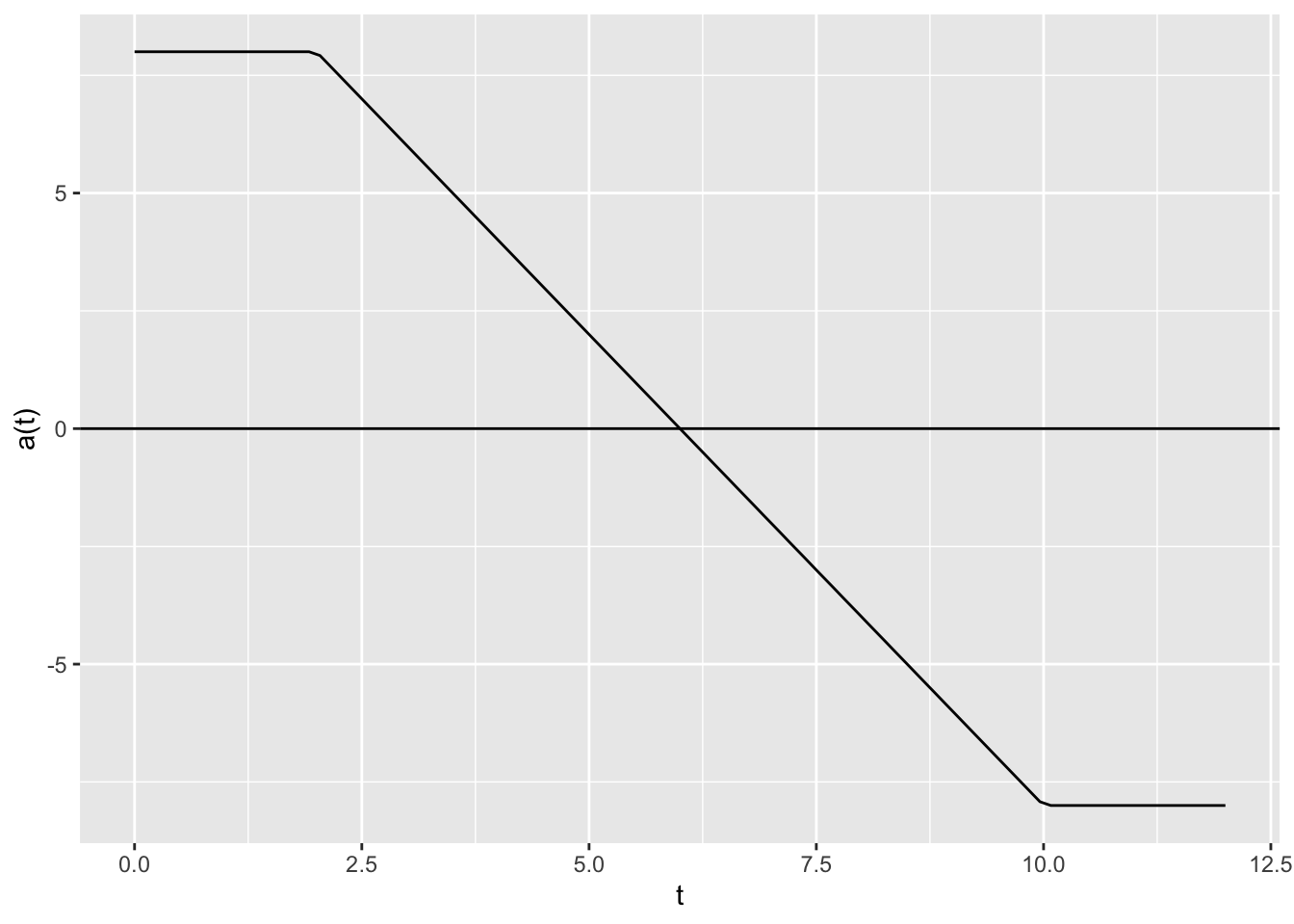
- Is the velocity increasing or decreasing at \(t=2\)? \(t=15\)?
- What happens when \(t=6\)?
- When else (besides \(t=0\)) is the velocity 55 feet per second?
- When is velocity at a global maximum?
- When is velocity at a global minimum?
Making Cupcakes
The marginal cost of making cupcakes is given by \[K'(q)=\frac{1}{100}q^2+\frac{1}{5}q+1,\] where \(q\) is in dozens of cupcakes.
- Set up a definite integral to calculate \(K(30)-K(0)\), which is the change in costs when we create 30 dozen cupcakes.
- Estimate this definite integral using RStudio.
- If our fixed costs are $1500, what is the total cost to make 30 dozen cupcakes?
Area Between Curves
Below is a graph of both \(\sin(x)\) and \(\cos(x)\) on the interval \([0,2\pi]\).
slice_plot(sin(x)~x, domain(x=0:2*pi)) %>%
slice_plot(cos(x)~x) +
scale_x_continuous(breaks=seq(0,2*pi,pi/4),labels=c("0", "\u03c0/4", "\u03c0/2", "3\u03c0/4", "\u03c0","5\u03c0/4", "3\u03c0/2", "7\u03c0/2", "2\u03c0"))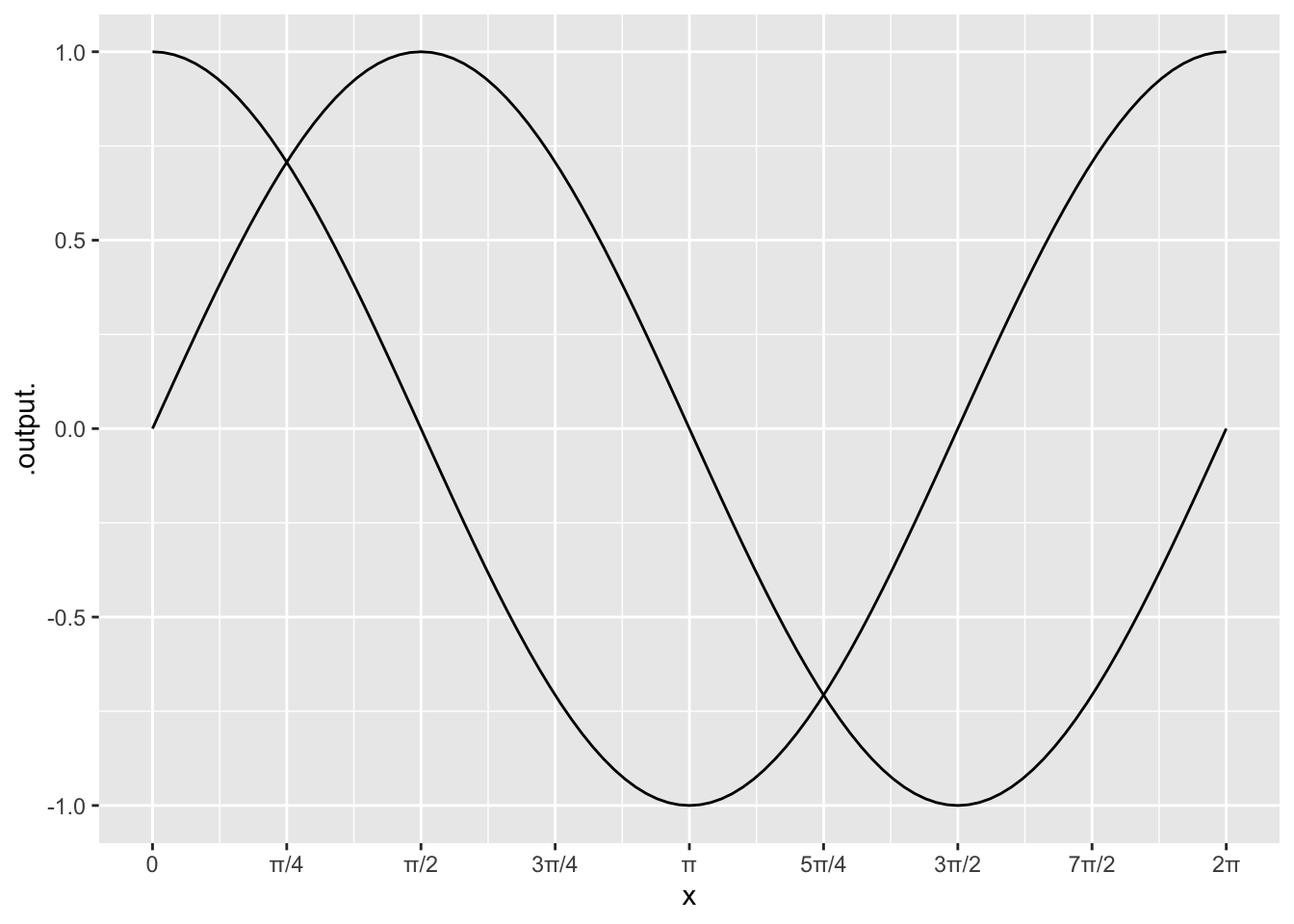
- Write a sum of integrals which represents the enclosed by the two curves.
Hint: \(\sin(x) = \cos(x)\) at \(x=\pi/4\) and \(x=5\pi/4\). - Use RStudio to estimate the area between these two curves.
Solutions
Drive My Car
- We approximate these definite integrals using 1000 subintervals.
- \(\displaystyle{\int_0^5 v(x)dx}\)
f=makeFun(-t+5 ~ t)
a = 0
b = 5
num = 1000
### the approximation of f(x) on interval [a,b]
base = (b-a)/num
points = seq(from=a+base, to=b, by=base)
heights = f(points)
areas = base*heights
sum(areas)## [1] 12.4875- \(\displaystyle{\int_0^8 v(x)dx}\)
f=makeFun(-t+5 ~ t)
a = 0
b = 8
num = 1000
### the approximation of f(x) on interval [a,b]
base = (b-a)/num
points = seq(from=a+base, to=b, by=base)
heights = f(points)
areas = base*heights
sum(areas)## [1] 7.968- \(\displaystyle{\int_0^{12} v(x)dx}\)
f=makeFun(-t+5 ~ t)
a = 0
b = 12
num = 1000
### the approximation of f(x) on interval [a,b]
base = (b-a)/num
points = seq(from=a+base, to=b, by=base)
heights = f(points)
areas = base*heights
sum(areas)## [1] -12.072The car turns around at \(t=5\). We have \(v(t) > 0\) for \(t < 5\) and \(v(t) < 0\) for \(t > 5\).
We must look at the signed area. When is the (positive) area above the \(x\)-axis equal to the (negative) area below the \(x\)-axis? This happens at \(t=12\). So this is the time that the car returns to where it started.
Accelerate My Car
See the class slides for a visual explanation of this problem. Here is a descriptive solution.
The car’s velocity is increasing at \(t=2\) because acceleration is positive. The car’s velocity is decreasing at \(t=15\) because acceleration is negative
At \(t=6\), the acceleration is zero. We accelerate up to this point, and we decelerate after this point. So it is a local maximum for velocity.
The velocity is 55 feet per second at \(t=12\) because the area above the \(x\)-axis (positive acceleration so far) equals the area below the \(x\)-axis (negative acceleration so far).
The maximum velocity occurs at \(t=6\)? The car accelerates for the first 6 seconds. Then it decelerates for the next 10 seconds (until \(t=16\)). Then it accelerates again for 2 seconds. However by \(t=18\), the total deceleration (area below the \(x\)-axis) is more than the total acceleration.
The minimum velocity occurs at \(t=12\). This is when we’ve seen the most deceleration, and we’ve decelerated more than we’ve accelerated.
Making Cupcakes
The marginal cost of making cupcakes is given by \[K'(q)=\frac{1}{100}q^2+\frac{1}{5}q+1,\] where \(q\) is in dozens of cupcakes.
- By the Fundamental Theorem of Calculus, the definite integral that calculates \(K(30)-K(0)\) is
\[\int_0^{30} K'(q) dq = \int_0^{30} \left( \frac{1}{100}q^2+\frac{1}{5}q+1 \right) dq \]
- Here is our RStudio estimate.
f=makeFun(1/100 * q^2 + 1/5*q + 1 ~ q)
a = 0
b = 30
num = 100000
### the approximation of f(x) on interval [a,b]
base = (b-a)/num
points = seq(from=a+base, to=b, by=base)
heights = f(points)
areas = base*heights
sum(areas)## [1] 210.0023- The total costs are approximate \(1500+210\), which is the sum of our fixed costs and our production costs.
Area Between Curves
The sine curve and the cosine curve intersect when \(x=\pi/4\) and \(x=5\pi/4\). The cosine curve is above the sine curve on \([0,\pi/4]\). Then the sine curve is on top on \([\pi/4,5\pi/4]\). Then cosine is back on top on \([5\pi/4, 2\pi\). So the area is \[\int_{\pi/4}^{5\pi/4} ( \cos(x) - \sin(x)) dx + \int_{\pi/4}^{5\pi/4} ( \sin(x) - \cos(x)) dx + \int_{5\pi/4}^{2\pi} ( \cos(x) - \sin(x)) dx.\]
Our RStudio estimates for each part are
f=makeFun(cos(x) - sin(x) ~ x)
a = 0
b = pi /4
num = 100000
### the approximation of f(x) on interval [a,b]
base = (b-a)/num
points = seq(from=a+base, to=b, by=base)
heights = f(points)
areas = base*heights
sum(areas)## [1] 0.4142096f=makeFun(sin(x) - cos(x) ~ x)
a = pi/4
b = 5* pi /4
num = 100000
### the approximation of f(x) on interval [a,b]
base = (b-a)/num
points = seq(from=a+base, to=b, by=base)
heights = f(points)
areas = base*heights
sum(areas)## [1] 2.828427f=makeFun(cos(x) - sin(x) ~ x)
a = 5*pi/4
b = 2*pi
num = 100000
### the approximation of f(x) on interval [a,b]
base = (b-a)/num
points = seq(from=a+base, to=b, by=base)
heights = f(points)
areas = base*heights
sum(areas)## [1] 2.414225So our estimate of the area is
0.414 + 2.828 + 2.414## [1] 5.656