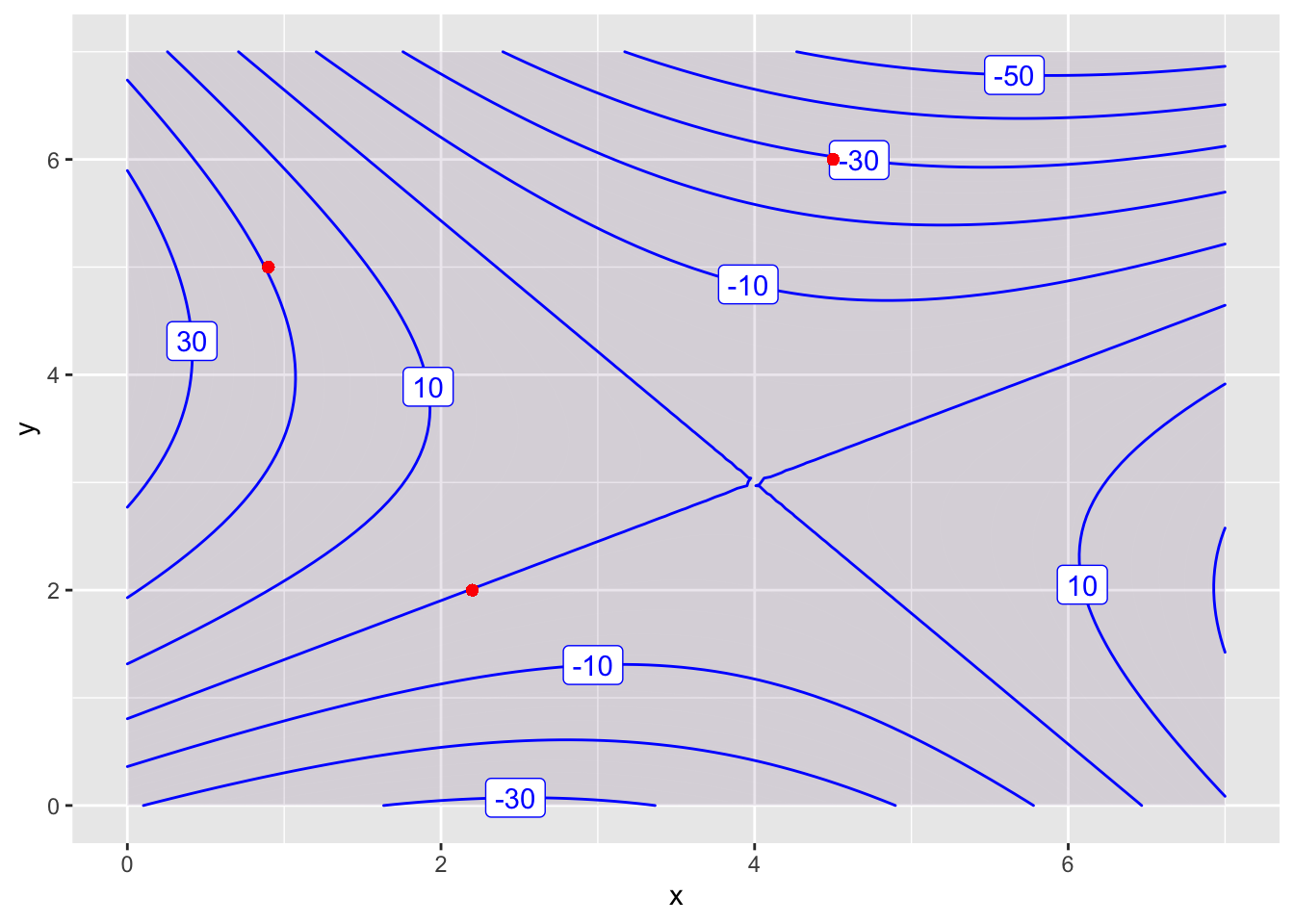
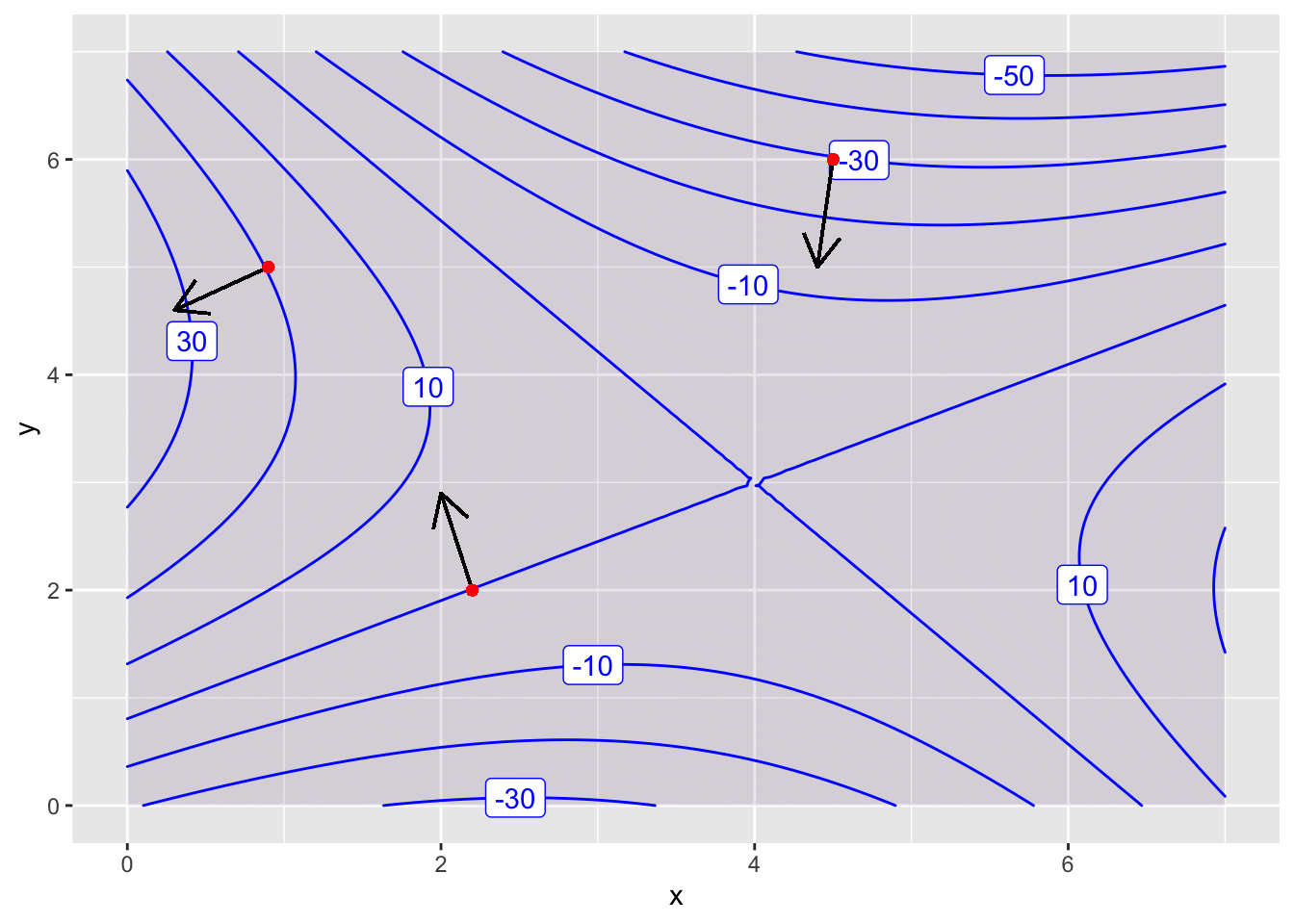
4.D The Gradient
Activities
Partial Derivative Practice
Find the partial derivatives \(f_x\) and \(f_y\) for each of these functions.
- \(f(x,y) = x^5 + x^2y^3 + y^4\)
- \(f(x,y) = e^x \sin(y) + \ln(y) \cos(x)\)
- \(f(x,y) = \ln (x^2 - y^2)\)
- \(f(x,y) = x^2 y^3 e^x \sin(y)\)
Second Partial Derivative Practice
For each of these functions, find the second partial derivatives \(f_{xx}, f_{yy}, f_{xy}\) and \(f_{yx}\). Confirm that \(f_{xy} = f_{yx}\)
- \(f(x,y) = 7x^3 + \cos(4y)\)
- \(f(x,y) = e^{2x+3y}\)
Gradient Practice
Calculate the gradient \(\nabla f(x,y)\) for each of these functions
- \(f(x,y) = 8x^2y^4\)
- \(\displaystyle{f(x,y) = \frac{x}{y}}\)
- \(f(x,y) = \ln(xy)\)
Solutions
Partial Derivative Practice
- \(f(x,y) = x^5 + x^2y^3 + y^4\)
\[ f_x = 5x^2 + 2xy^3 \qquad \qquad f_y = 3x^2y^2 + 4y^3 \]
- \(f(x,y) = e^x \sin(y) + \ln(y) \cos(x)\)
\[ f_x = e^x \sin(y) - \ln(y) \sin(x) \qquad \qquad f_y = e^x \cos(y) + \frac{1}{y} \cos(x) \]
- \(f(x,y) = \ln (x^2 - y^2)\)
\[ f_x = \frac{2x}{x^2-y^2} \qquad \qquad f_y = - \frac{2y}{x^2-y^2} \]
- \(f(x,y) = x^2 y^3 e^x \sin(y)\)
Let’s rewrite this function as \(x^2 e^x y^3 \sin(y)\)
\[ f_x = (2xe^x + x^2e^x) y^3\sin(y) \qquad \qquad f_y = (3y^2 \sin(y) - y^3 \cos(y)) x^2 e^x \]
Second Partial Derivative Practice
- \(f(x,y) = 7x^3 + \cos(4y)\)
\[\begin{align*} f_x &= 21 x^2 \\ f_{xx} &= 42 x \\ f_{xy} &= 0 \\ \\ f_y &= -4 \sin(4y) \\ f_{yy} &= -16 \cos(y) \\ f_{yx} &=0 \end{align*}\]
- \(f(x,y) = e^{2x+3y}\)
\[\begin{align*} f_x &= 2e^{2x+3y} \\ f_{xx} &= 4e^{2x+3y} \\ f_{xy} &= 6e^{2x+3y} \\ \\ f_y &= 3e^{2x+3y} \\ f_{yy} &= 9e^{2x+3y} \\ f_{yx} &= 6e^{2x+3y} \end{align*}\]
Gradient Practice
Calculate the gradient \(\nabla f(x,y)\) for each of these functions
- \(\nabla f(x,y) = \langle 16x y^4, 32x^2y^3 \rangle\)
- \(\nabla f(x,y) = \langle y^{-1}, -xy^{-2} \rangle\)
- \(f(x,y) = \langle x^{-1}, y^{-1} \rangle\)