3.C Partial Derivatives
Activities
Estimating From Data
The maximum duration of a scuba dive \(T(V,D)\) (in minutes) depends on the volume \(V\) of air (at sea-level pressure) in the tank and the depth \(D\) (in feet) of the dive. The following table shows the estimated dive times for various combinations of air volume and dive depth.
| Dive Time (minutes) | Air Volume | ||||
| 20 ft3 | 40 ft3 | 60 ft3 | 80 ft3 | ||
| Depth | 20 ft | 12.5 | 25.0 | 37.5 | 50.0 |
| 40 ft | 9.0 | 18.0 | 27.0 | 36.0 | |
| 60 ft | 7.1 | 14.2 | 21.3 | 28.4 | |
| 80 ft | 5.8 | 11.6 | 17.4 | 23.2 | |
Use this table to estimate the derivatives \(\displaystyle{\frac{\partial T}{\partial V}}\) and \(\displaystyle{\frac{\partial T}{\partial D}}\) at the point \((V=60, T=40)\). Give units for each of these derivatives and then interpret what these numbers mean.
Estimating From a Contour Plot
The production function \(F(L,K)\) for a factory gives the number of units produced by labor \(L\) and capital \(K\) (both measured in dollars). This production function is given by \[ F(L,K) = 10 L^{2/7}K^{5/7}. \] Here is a contour plot of the production function.
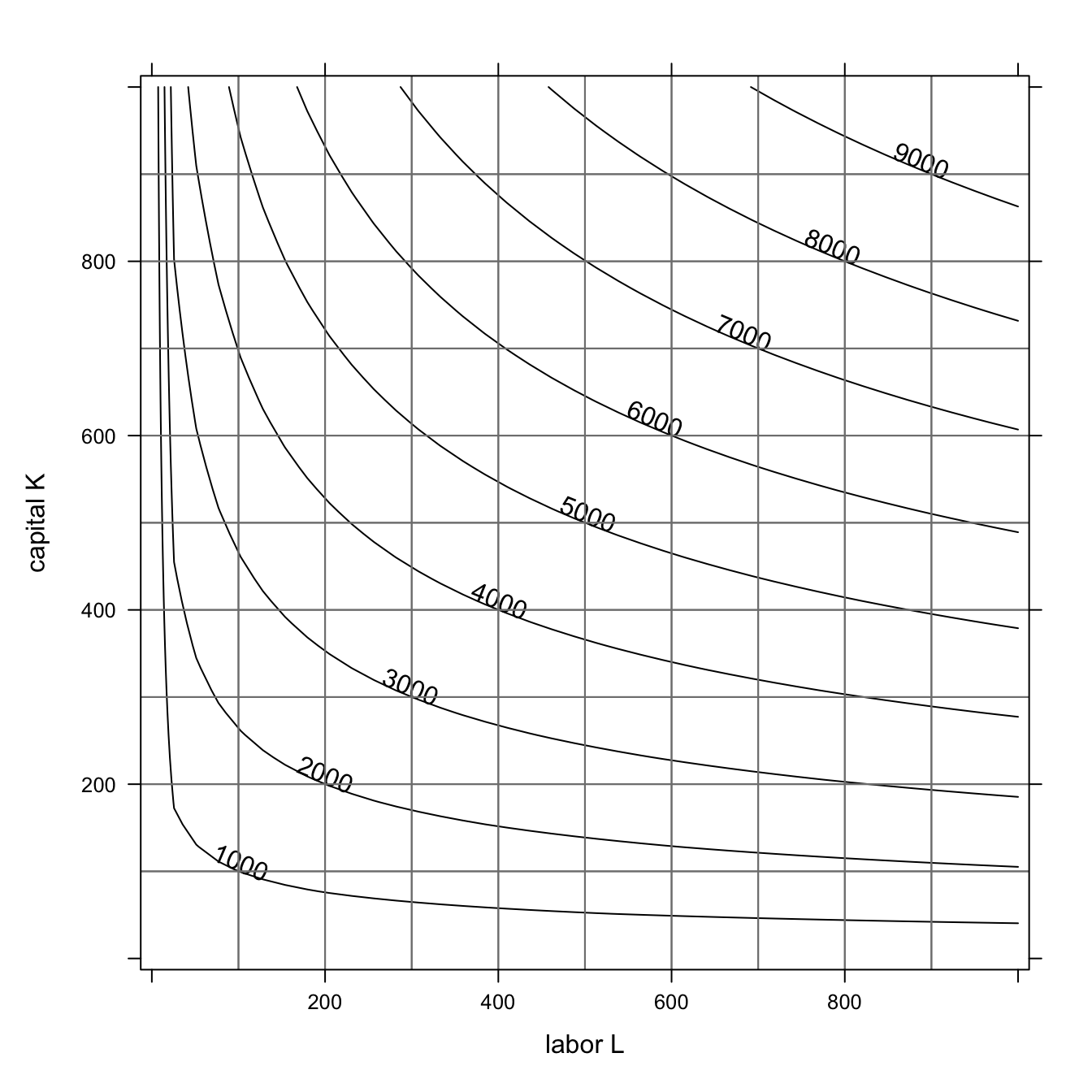
- Estimate the production output for \(L=400\) and \(K=600\).
- Estimate the partial derivative \(\displaystyle{\frac{\partial F}{\partial L}}\) at \((400,600)\).
- Estimate the partial derivative \(\displaystyle{\frac{\partial F}{\partial K}}\) at \((400,600)\).
Estimating Using Desmos
Use desmos to define the prodution function \(F(L,K) = L^{2/7} K^{5/7}\) from the previous problem and to answer the analogous questions
- Calculate the production outpuut \(F(400,600)\).
- Estimate the partial derivative \(\displaystyle{\frac{\partial F}{\partial L}}\) at \((400,600)\). Your answer must be correct to two decimal places.
- Estimate the partial derivative \(\displaystyle{\frac{\partial F}{\partial K}}\) at \((400,600)\). Your answer must be correct to two decimal places.
Compare your three answers to the estimates from the contour plot in the previous problem.
Solutions
Estimating From Data
We estimate the partial derivatives. We have \[ T_V(60,40) \approx \frac{T(80,40) - T(60,40)}{80-60} = \frac{36 - 27}{80-60} = \frac{9}{20} = 0.45 \mbox{ min/ft}^3 \] where we have used the interval \(60 \leq V \leq 80\) for our estimate. We could also use \(40 \leq V \leq 80\) or \(40 \leq V \leq 80\) as the interval for our estimate. \[ T_D(60,40) \approx \frac{T(60,60) - T(60,40)}{60-40} = \frac{21.3 - 27}{60-40} = - \frac{5.7}{20} = -0.285 \mbox{ min/ft} \] where we have used the interval \(40 \leq D \leq 60\) for our estimate. We could also use \(20 \leq D \leq 40\) or \(20 \leq D \leq 60\) as the interval for our estimate.
The units for \(T_V(V,D)\) are minutes per cubic feet. An additional cubic foot of air will allow you to dive for an extra 0.45 minutes.
The units for \(T_V(V,D)\) are minutes per feet. An additional foot of dive depth will reduce your dive time: the change is \(-0.285\) minutes.
Estimating From a Contour Plot
We have \[ F(400,600) \approx 5300. \]
Let’s estimate by using the contour line \(F(L,K) = 5000\). I estimate that \(F(325,600)=5000\) and that \(F(400,550)=5000\). Therefore
\[ F_L(400,600) \approx \frac{5300 - 5000}{400 - 325} = \frac{300}{75} = 4 \] and \[ F_K(400,600) \approx \frac{5300 - 5000}{600-550} = \frac{300}{50} = 6. \]
Estimating Using Desmos
Here is a link to my desmos calculations.
- \(F(400,600) = 534.37\)
- \(F_L(400,600) = 0.38\)
- \(F(400,600) = 0.64\)