5.A 1D Optimization
Activities
Characterize the Extrema
- Each of the functions below is defined on \((-\infty, \infty)\). Find all the local extrema and global extrema.
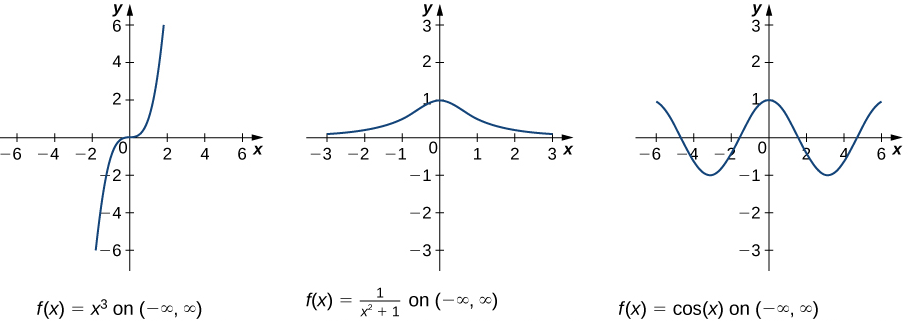
image: https://openstax.org/books/calculus-volume-1/pages/4-3-maxima-and-minima
- Each of the functions below is defined on a finite interval. Find all the local extrema and global extrema.
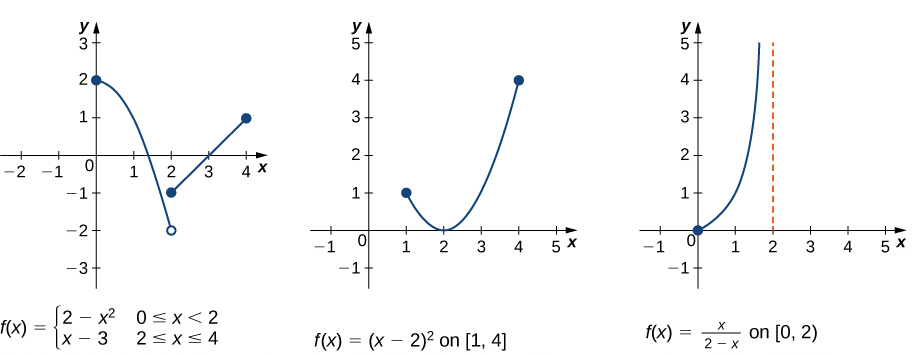 image: https://openstax.org/books/calculus-volume-1/pages/4-3-maxima-and-minima
image: https://openstax.org/books/calculus-volume-1/pages/4-3-maxima-and-minima
First Derivative Test
Find the critical point(s) of the following functions. Then use the first derivative test to determine whether it is a local minimum, a local maximum, or neither
- \(f(x) = x - e^x\)
- \(g(x) = x + \sin(x)\) on \([0,2\pi]\)
Second Derivative Test
The function \(f(x) = x^4-8 x^3+22 x^2-24 x\) has critical points at \(x=1\) and \(x=2\) and \(x=3\).
- Find \(f''(x)\).
- Use the second derivative test to determine whether each of the critical points is a minimum or a maximum.
Cupcake Store
A cupcake store finds that at a price of $4.00, the demand is 400 cupcakes. For every $.25 decrease in price, the demand increases by 20 cupcakes.
- Define a function \(q(x)\) that gives the demand for cupcakes at a price of \(x\) dollars.
- The revenue for a price of \(x\) dollars is \(r(x) = x \cdot q(x)\). Use your function from part (a) to find the price that maximizes revenue.
Find the price and quantity that maximize the revenue.
Solutions
Characterize the Extrema
- We have three different functions
- \(f(x) = x^3\) has no extrema
- \(f(x) = \frac{1}{x^2+1}\) has a global maximum at \(x=1\)
- \(f(x) = \cos(x)\) has global maxima at \(x=2k \pi\) for every integer \(k\). It has global minima at \(x=(2k+1) \pi\) for every integer \(k\).
- Once again we have three functions
- LEFT: global maximum at \(x=0\); local maximum at \(x=4\). Note that \(x=2\) is not a local minimum.
- MIDDLE: local maximum at \(x=1\); global minimum at \(x=2\); global maximum at \(x=4\).
- RIGHT: global minimum at \(x=0\). Note that \(x=2\) is not a global maximum (because the function is not defined at \(x=2\)).
First Derivative Test
Find the critical point(s) of the following functions. Then use the first derivative test to determine whether it is a local minimum, a local maximum, or neither
We have \(f(x) = x - e^x\) and so \(f'(x) = 1 - e^x\). There is one critical point: \[ \begin{array}{rcl} 1-e^x &=& 0 \\ e^x &=& 1 \\ x &=& 0. \end{array} \] Using the first derivative test, we have \(f'(-1) = 1 - e^{-1} > 0\) and \(f'(1) = 1 - e < 0\). Therefore \(x=0\) is a local maximum.
We have \(g(x) = x + \sin(x)\) and therefore \(g'(x) = 1 + \sin(x)\). There is one critical point: \[ \begin{array}{rcl} 1 + \cos(x) &=& 0 \\ \cos(x) &=& -1 \\ x &=& \pi \end{array} \]
We have \(g'(\pi/2) = 1 > 0\) and \(g'(3 \pi/2) = 1 > 0\). (In fact, \(1+\cos(x)\) is never negative) Therefore this point is not an extremum.
To find all the extrema of \(g(x)\), we need to consider the endpoints of \([0,2\pi]\). The function never decreases as we move from \(0\) to \(2\pi\).So \(x=0\) is the global minimum, and \(x=2\pi\) is the global maximum.
Second Derivative Test
The function \(f(x) = x^4-8 x^3+22 x^2-24 x\) has critical points at \(x=1\) and \(x=2\) and \(x=3\).
- We have \[f'(x) = 4x^3 - 24 x^2 + 44 x - 24\] and \[ f''(x) = 12x^2 - 48x + 44.\]
- We check the critical points \(x=1\), \(x=2\) and \(x=3\). \[ \begin{array}{rcl} f''(1) &=& 12 - 48 + 44 = 8 > 0 \\ f''(2) &=& 48 - 96 + 44 = -2 < 0 \\ f''(3) &=& 108 - 144 + 44 > 0 \\ \end{array} \]
Therefore \(x=1\) and \(x=3\) are local minima and \(x=2\) is a local maximum.
Cupcake Store
A cupcake store finds that at a price of $4.00, the demand is 400 cupcakes. For every $.25 decrease in price, the demand increases by 20 cupcakes.
The description of the demand function tells us that \(q(x)\) is a linear function with a negative slope. The slope is \(20/(-.25)=-80\). So \(q(x) = -80x + c\) and we can determine \(c\) by using the fact that \(q(4)=400\). We have \[ 400 = -80 \cdot 4 + c = -320 + c \] so \(c=720\). In conclusion, our demand function is \[q(x) = -80x + 720.\]
The revenue at price \(x\) is \[r(x) = x q(x) = x \left(-80x + 720 \right) = -80x^2 + 720x.\] Taking the derivative and solving for critical points gives \[ -160 x + 720 = 0 \] and therefore \(x=720/160= 4.5\). By the second derivative test, this is a local maximum.
We sell \(q(4.5) = 400 - 40 = 360\) cupcakes and obtain revenue \(r(4.5) = 4.5 \cdot 360 = 1620\).