Vector 29 Quiz 2 Review

29.1 Overview

Our second quiz covers sections 2.1 - 2.3 and 4.1-4.6 in Lay’s book. This corresponds to Problem Sets 4 and 5.

The best way to study is to do practice problems. The Quiz will have calculation problems (like Edfinity) and more conceptual problems (like the problem sets). Here are some ways to practice:

Make sure that you have mastered the Vocabulary, Skills and Concepts listed below.
Look over the Edfinity homework assingments
Do practice problems from the Edfinity Practice assignments. These allow you to “Practice Similar” by generating new variations of the same problem.
Redo the Jamboard problems
Try to resolve the Problem Sets and compare your answers to the solutions.
Do the practice problems below. Compare your answers to the solutions.

29.1.1 Vocabulary and Concepts

You should understand these concepts and be able to read and use these terms correctly:

all of the Important Definitions found here.
matrix inverses
the Invertible Matrix Theorem
homogeneous coordinates
subspaces
null space and column space of a matrix
kernel and image of a linear transformation
basis (span and linearly independent)
coordinate vector with respect to a basis $\mathcal{B}$
change-of-coordinates matrix
dimension

29.1.2 Skills

You should be able to perform these linear algebra tasks.

solve matrix algebra equations
find a matrix inverse
use homogeneous coordinates to transform and translate images in the plane.
show that a subset is a subspace or demonstrate that it is not a subspace
describe the null space and the column space
determine if a vector is in a null space or column space
find a basis of a subspace
answer questions about the connections between all these ideas
write short proofs of basic statements using the Important Definitions

29.2 Practice Problems

29.2.1

Here is a picture of some boats.

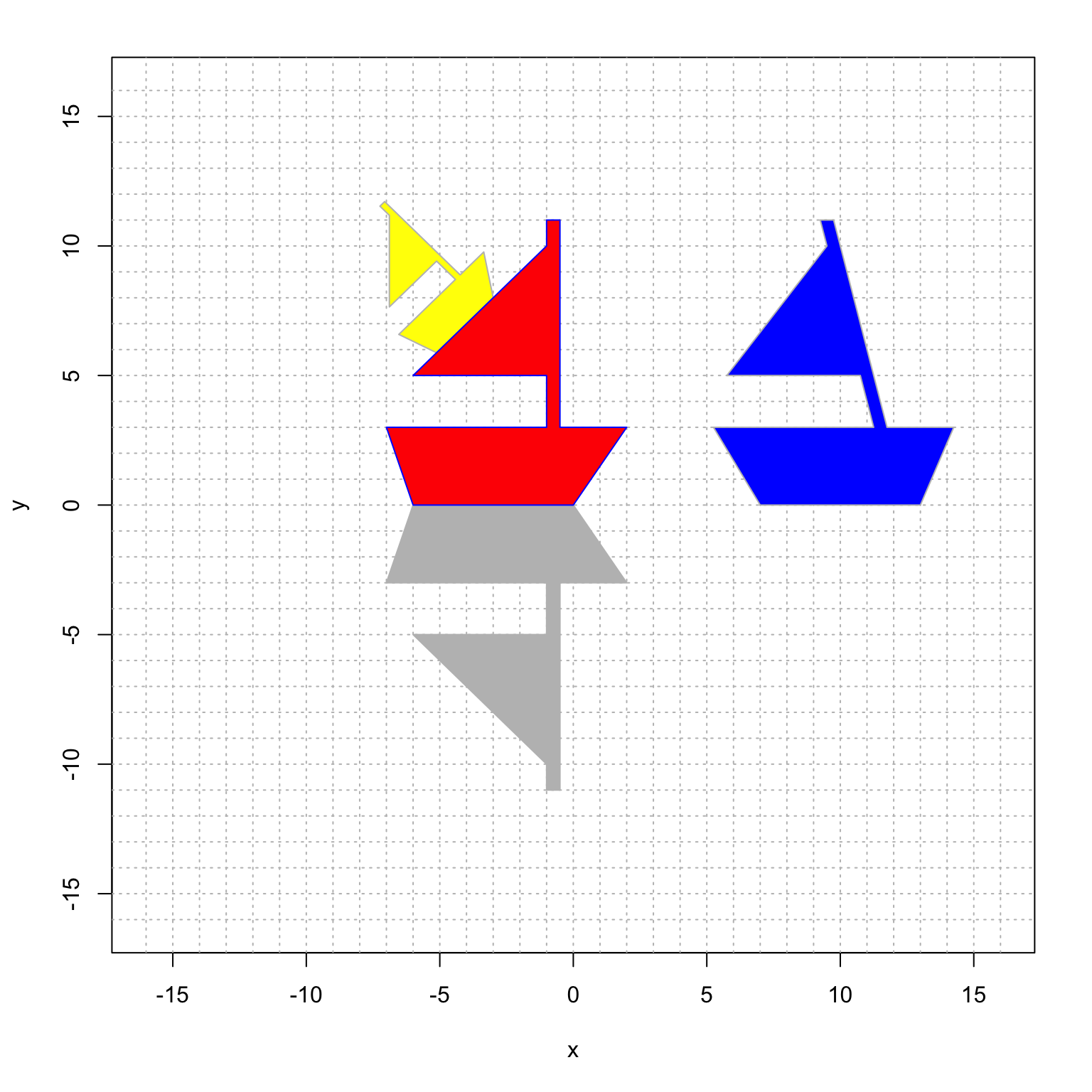
The blue, yellow and gray boats are linear transformations of the red boat (using homogeneous coordinates). Find the $3 \times 3$ matrix corresponding to the linear transformation that creates:

The shadow gray boat
The fast blue boat
The funny yellow boat.

For your convenience, here is the code to draw the red boat as well as some commented code that you can adapt to create the other boats.

'```{r,fig.height=4,fig.width=4}

# the red boat
boat =cbind(c(0,0), c(-6,0), c(-7,3), c(-1,3), c(-1,5), c(-6,5), c(-1,10), c(-1,11),
            c(-.5,11), c(-.5,3), c(2,3) )
boat = rbind(boat,rep(1,11))

##### update these matrices
graymap = cbind(c(1,0,0), c(0,1,0),c(0,0,1))
bluemap = cbind(c(1,0,0), c(0,1,0),c(0,0,1))
yellowmap = cbind(c(1,0,0), c(0,1,0),c(0,0,1))


# plot all of the boats
grayboat = graymap %*%  boat
blueboat = bluemap %*%  boat
yellowboat = yellowmap %*%  boat

plot(boat[1,],boat[2,],type="n",xlim=c(-16,16),ylim=c(-16,16),xlab="x",ylab="y")
abline(h=-16:16, v=-16:16, col="gray", lty="dotted")

polygon(grayboat[1,], grayboat[2,], col = "gray", border = "gray")
polygon(blueboat[1,], blueboat[2,], col = "blue", border = "gray")
polygon(yellowboat[1,], yellowboat[2,], col = "yellow", border = "gray")
polygon(boat[1,], boat[2,], col = "red", border = "blue")

29.2.2

Find the inverse of the matrix \[ \left[ \begin{array}{rrr} 1 & -2 & 2 \\ 1 & 0 & 0 \\ 2 &-4 & 5 \end{array} \right] \]

29.2.3

Suppose that a linear transformation $T: \mathbb{R}^n \rightarrow \mathbb{R}^n$ has the property that $T(\mathsf{u}) = T(\mathsf{v})$ for some pair of distinct vectors $\mathsf{u}, \mathsf{v} \in \mathbb{R}^n$. Can $T$ map $\mathbb{R}^n$ onto $\mathbb{R}^n$? Why or why not?

29.2.4

Let $U$ and $W$ be subspaces of a vector space $\mathbb{R}^n$. Prove or disprove the following statements a. $U \cap W = \{ \mathsf{v} \in \mathbb{R}^n \mid \mathsf{v} \in U \mbox{ and } \mathsf{v} \in W \}$ is a subspace b. $U \cup W = \{ \mathsf{v} \in \mathbb{R}^n \mid \mathsf{v} \in U \mbox{ or } \mathsf{v} \in W \}$ is a subspace c. $U+W = \{\mathsf{u} + \mathsf{w} \mid \mathsf{u} \in U \mbox{ and } \mathsf{w} \in W \}$ is a subspace

29.2.5

Let $T: \mathbb{R}^n \rightarrow \mathbb{R}^m$ be a linear transformation.

Suppose that $T: \mathbb{R}^n \to \mathbb{R}^m$ is one-to-one. Prove that if $\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3$ are linearly independent, then $T(\mathsf{v}_1), T(\mathsf{v}_2), T(\mathsf{v}_3)$ are linearly independent.
Suppose that $T: \mathbb{R}^n \to \mathbb{R}^m$ is onto. Prove that if $\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3$ span $\mathbb{R}^n$ then $T(\mathsf{v}_1), T(\mathsf{v}_2), T(\mathsf{v}_3)$ span $\mathbb{R}^m$.

29.2.6

I have performed some row operations below for you on a matrix $A$. Find a basis for the column space and the null space of $A$. \[ A= \left[ \begin{matrix} 1& 2& 0& 2& 0& -1 \\ 1& 2& 1& 1& 0& -2 \\ 2& 4& -2& 6& 1& 2 \\ 1& 2& 0& 2& -1& -3 \\ \end{matrix}\right] \longrightarrow \left[ \begin{matrix} 1& 2& 0& 2& 0& -1\\ 0& 0& 1& -1& 0& -1\\ 0& 0& 0& 0& 1& 2\\ 0& 0& 0& 0& 0& 0\\ \end{matrix}\right] \]

29.2.7

Consider the matrix \[ A = \left[ \begin{array}{cccc} 1 & 5 & 2 & -4 \\ 3 & 10 & 2 & 8 \\ 4 & 15 & 4 & 4 \end{array} \right] \] Find a basis for $\mathrm{Col}(A)$. Find a basis for $\mathrm{Nul}(A)$.

29.2.8

Are the vectors in ${\mathcal B}$ a basis of $\mathbb{R}^3$? If not, find a basis of $\mathbb{R}^3$ that consists of as many of the vectors from ${\mathcal B}$ as is possible. Explain your reasoning. \[ \mathcal{B}=\left\{ \begin{bmatrix} 1 \\ -1 \\ -2 \end{bmatrix},\begin{bmatrix} 2 \\ -1 \\ 1 \end{bmatrix},\begin{bmatrix} -1 \\ -1 \\ -8 \end{bmatrix} \right\} \]

29.2.9

I have the vectors below: \[ \begin{bmatrix} 5\\ 4\\ 3\\ 1\\ 2 \end{bmatrix}, \begin{bmatrix} 4\\ 4\\ 3\\ 1\\ 2 \end{bmatrix}, \begin{bmatrix} 1\\ 1\\ 1\\ 1\\ 1\end{bmatrix}. \] I know that they do not span $\mathbb{R}^5$, but I want to extend them to a basis of $\mathbb{R}^5$ by adding some vectors to the set. I created the matrix below and row reduced. Give a basis for $\mathbb{R}^5$ that uses my three vectors and explain why this method works in general. \[ \left[ \begin{array}{cccccccc} 5 & 4 & 1 & 1 & 0 & 0 & 0 & 0 \\ 4 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \\ 3 & 3 & 1 & 0 & 0 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 & 1 & 0 \\ 2 & 2 & 1 & 0 & 0 & 0 & 0 & 1 \\ \end{array} \right] \rightarrow \left[ \begin{array}{cccccccc} 1 & 0 & 0 & 1 & 0 & 0 & 2 & -3 \\ 0 & 1 & 0 & -1 & 0 & 0 & -3 & 4 \\ 0 & 0 & 1 & 0 & 0 & 0 & 2 & -1 \\ 0 & 0 & 0 & 0 & 1 & 0 & 2 & -3 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & -2 \\ \end{array} \right] \]

29.2.10

Find the coordinates of $\mathsf{w}$ in the standard basis and of $\mathsf{v}$ in the $\mathcal{B}$-basis. \[ \mathcal{B} = \left\{ \mathsf{v}_1=\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \mathsf{v}_2=\begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix}, \mathsf{v}_3=\begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \end{bmatrix}, \mathsf{v}_4=\begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \right\}, \qquad \mathsf{w} = \begin{bmatrix} 3 \\ -2 \\ 0 \\ -1 \end{bmatrix}_{\mathcal{B}}, \qquad \mathsf{v} = \begin{bmatrix} 10 \\ 9 \\ 7 \\ 4 \end{bmatrix}_{\mathcal{S}} \]

29.2.11

The subspace $S \subset \mathbb{R}^5$ is given by \[ \mathsf{S} = \mathsf{span} \left( \begin{bmatrix}1\\ 1\\ 0\\ -1\\ 2 \end{bmatrix}, \begin{bmatrix} 0\\ 1\\ 1\\ 1\\ 1 \end{bmatrix}, \begin{bmatrix} 3\\ 1\\ -2\\ -5\\ 4 \end{bmatrix}, \begin{bmatrix} 1\\ 0\\ 1\\ 0\\ 1 \end{bmatrix}, \begin{bmatrix} 2\\ -1\\ -1\\ -3\\ 1 \end{bmatrix}, \right)\]

Use the following matrix to find a basis for $S$. What is the dimension of $S$? \[ A=\left[ \begin{array}{ccccc} 1 & 0 & 3 & 1 & 2 \\ 1 & 1 & 1 & 0 & -1 \\ 0 & 1 & -2 & 1 & -1 \\ -1 & 1 & -5 & 0 & -3 \\ 2 & 1 & 4 & 1 & 1 \\ \end{array} \right] \rightarrow \left[ \begin{array}{ccccc} 1 & 0 & 3 & 0 & 1 \\ 0 & 1 & -2 & 0 & -2 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} \right] \]
Find a basis for $\mathrm{Nul}(A)$. What is the dimension of this nullspace?

29.2.12

A $6 \times 8$ matrix $A$ contains 5 pivots. For each of $\mathrm{Col}(A)$ and $\mathrm{Nul}(A)$,

Determine the dimension of the subspace,
Indicate whether it is subspace of $\mathbb{R}^6$ or $\mathbb{R}^8$, and
Decide how you would find a basis of the subspace.

29.3 Solutions to Practice Problems

29.3.1

Here are the matrices to make the boats.

Shadow gray boat: \[ \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
Fast blue boat: \[ \begin{bmatrix} 1 & -0.25 & 13 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
Funny yellow boat: \[ \begin{bmatrix} 0.35 & -0.35 & -3 \\ 0.35 & 0.35 & 8 \\ 0 & 0 & 1 \end{bmatrix} \]

And here is the updated code

'```{r,fig.height=4,fig.width=4,echo=TRUE}

# the red boat
boat =cbind(c(0,0), c(-6,0), c(-7,3), c(-1,3), c(-1,5), c(-6,5), c(-1,10), c(-1,11),
            c(-.5,11), c(-.5,3), c(2,3) )
boat = rbind(boat,rep(1,11))


# updated mappings
graymap = cbind(c(1,0,0), c(0,-1,0),c(0,0,1))
bluemap = cbind(c(1,0,0), c(0,1,0),c(13,0,1))  %*% cbind(c(1,0,0), c(-.25,1,0),c(0,0,1))
t=pi/4
yellowmap = cbind(c(1,0,0), c(0,1,0),c(-3,8,1)) %*% cbind(c(cos(t),sin(t),0), c(-sin(t),cos(t),0),c(0,0,1)) %*% cbind(c(1/2,0,0),c(0,1/2,0),c(0,0,1))



# plot all of the boats
grayboat = graymap %*%  boat
blueboat = bluemap %*%  boat
yellowboat = yellowmap %*%  boat

plot(boat[1,],boat[2,],type="n",xlim=c(-16,16),ylim=c(-16,16),xlab="x",ylab="y")
abline(h=-16:16, v=-16:16, col="gray", lty="dotted")

polygon(grayboat[1,], grayboat[2,], col = "gray", border = "gray")
polygon(blueboat[1,], blueboat[2,], col = "blue", border = "gray")
polygon(yellowboat[1,], yellowboat[2,], col = "yellow", border = "gray")
polygon(boat[1,], boat[2,], col = "red", border = "blue")

29.3.2

The inverse is \[ \begin{bmatrix} 0 & 1 & 0 \\ -5/2 & 1/2 &1 \\ -2 & 0 & 1 \end{bmatrix} \]

require(pracma)
A = cbind(c(1,1,2),c(-2,0,-4),c(2,0,5),c(1,0,0),c(0,1,0),c(0,0,1))
 rref(A)

##      [,1] [,2] [,3] [,4] [,5] [,6]
## [1,]    1    0    0  0.0  1.0    0
## [2,]    0    1    0 -2.5  0.5    1
## [3,]    0    0    1 -2.0  0.0    1

29.3.3

No $T$ cannot be an onto mapping by the Invertible Matrix Theorem. Since $T$ is not one-to-one, the mapping cannot be onto.

29.3.4

True

Since $U$ and $W$ are subspaces, we know that $\mathbb{0} \in U$ and $\mathbb{0} \in W$. Therefore $\mathbb{0} \in U \cap W$.
Let $\mathsf{v}_1 \in U \cap W$ and $\mathsf{v}_2 \in U \cap W$.
We know that $\mathsf{v}_1 \in U$ and $\mathsf{v}_2 \in U$. Since $U$ is a subspace, we have $\mathsf{v}_1 + \mathsf{v}_2 \in U$.
We know that $\mathsf{v}_1 \in W$ and $\mathsf{v}_2 \in W$. Since $W$ is a subspace, we have $\mathsf{v}_1 + \mathsf{v}_2 \in W$. Therefore $\mathsf{v}_1 + \mathsf{v}_2 \in U \cap W$.
Let $\mathsf{v} \in U \cap W$ and $c \in \mathbb{R}$.
We know that $\mathsf{v} \in U$ and $c \in R$. Since $U$ is a subspace, we have $c \mathsf{v} \in U$.
We know that $\mathsf{v} \in W$ and $c \in R$. Since $W$ is a subspace, we have $c \mathsf{v} \in W$.
Therefore $c \mathsf{v} \in U \cap W$.

False. Here is an example that shows this is not always true. Let $V= \mathbb{R}^2$, $U = \{ { x \choose 0} \mid x \in \mathbb{R} \}$ and $W= \{ { 0 \choose y} \mid y \in \mathbb{R} \}$. The set $U \cup W$ is not closed under addition. For example, ${1 \choose 0} + {0 \choose 1} = { 1 \choose 1} \notin U \cup W$.
True.

Since $U$ and $W$ are subspaces, we know that $\mathbb{0} \in U$ and $\mathbb{0} \in W$. Therefore $\mathbb{0} = \mathbb{0} + \mathbb{0} \in U + W$.
Let $\mathsf{u}_1 + \mathsf{w}_1 \in U + W$ and $\mathsf{u}_1 + \mathsf{w}_2 \in U + W$, where $\mathsf{u}_1, \mathsf{u}_2 \in U$ and $\mathsf{w}_1, \mathsf{w}_2 \in W$. Then \[ (\mathsf{u}_1 + \mathsf{w}_1) + (\mathsf{u}_2 + \mathsf{w}_2) = (\mathsf{u}_1 + \mathsf{u}_2) + (\mathsf{w}_1 + \mathsf{w}_2) \] and $\mathsf{u}_3 = (\mathsf{u}_1 + \mathsf{u}_2) \in U$ (because $U$ is a subspace) and $\mathsf{w}_3 = (\mathsf{w}_1 + \mathsf{w}_2) \in W$ (because $W$ is a subspace).
Therefore $(\mathsf{u}_1 + \mathsf{v}_1) + (\mathsf{u}_2 + \mathsf{w}_2) = \mathsf{u}_3 + \mathsf{w}_3 \in U + W$.
Let $\mathsf{u} + \mathsf{w} \in U + W$ and $c \in \mathbb{R}$. Then $c(\mathsf{u} + \mathsf{w}) = c \mathsf{u} + c \mathsf{w}$. We know that $c \mathsf{u} \in U$ (since $U$ is a subspace) and $c \mathsf{w} \in W$ (since $W$ is a subspace). Therefore $c(\mathsf{u} + \mathsf{w}) = c \mathsf{u} + c \mathsf{w} \in U+W$.

29.3.5

Suppose that $c_1 T(\mathsf{v}_1) + c_2 T(\mathsf{v}_2) + c_3 T(\mathsf{v}_3) = 0$. We must show that $c_1 = c_2 = c_3 = 0$.

Since $T$ is a linear transformation, this means that $T(c_1 \mathsf{v}_1+ c_2 \mathsf{v}_2 + c_3 \mathsf{v}_3 )= 0$.
Since $T$ is one-to-one and $T(\mathbf{0}) = \mathbf{0}$, we must have $c_1 \mathsf{v}_1+ c_2 \mathsf{v}_2 + c_3 \mathsf{v}_3 = \mathbf{0}$.
Because $\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3$ are linearly independent, this means that $c_1 = c_2 = c_3 = 0$.

This proves that $T(\mathsf{v}_1), T(\mathsf{v}_2), T(\mathsf{v}_3)$ are linearly independent.

Given $\mathsf{w} \in W$. We must show that there exist constants $c_1, c_2, c_3$ such that $\mathsf{w} = c_1 T(\mathsf{v}_1) + c_2 T(\mathsf{v}_2) + c_3 T(\mathsf{v}_3)$. Here we go!

Since $T$ is onto, we know that there exists $\mathsf{v} \in \mathbb{R}^n$ such that $T(\mathsf{v}) = \mathsf{w}$.
Since $\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3$ span $\mathbb{R}^n$, we know that there exist constants $c_1, c_2, c_3$ such that $\mathsf{v}= c_1 \mathsf{v}_1 + c_2 \mathsf{v}_2 + c_3 \mathsf{v}_k$
Therefore \[ \mathsf{w} = T(\mathsf{v})= T(c_1 \mathsf{v}_1 + c_2 \mathsf{v}_2 + c_3 \mathsf{v}_k) = c_1 T(\mathsf{v}_1) + c_2 T(\mathsf{v}_2) + c_3 T(\mathsf{v}_k) \] because $T$ is a linear transformation. This proves that $T(\mathsf{v}_1), T(\mathsf{v}_2), T(\mathsf{v}_3)$ span $W$.

29.3.6

A basis for $\mathrm{Col}(A)$ is \[ \begin{bmatrix} 1 \\1 \\ 2 \\ 1 \end{bmatrix}, \quad \begin{bmatrix} 0 \\1 \\ -2 \\ 0 \end{bmatrix}, \quad \begin{bmatrix} 0 \\0 \\ 1 \\ -1 \end{bmatrix} \] and a basis for $\mathrm{Nul}(A)$ is \[ \begin{bmatrix} -2 \\1 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \quad \begin{bmatrix} -2 \\0 \\ 1 \\ 1 \\ 0 \\ 0 \end{bmatrix}, \quad \begin{bmatrix} 1 \\0 \\ 1\\ 0 \\ -2 \\ 1 \end{bmatrix}. \]

29.3.7

Using RStudio we find:

##      [,1] [,2] [,3] [,4]
## [1,]    1    5    2   -4
## [2,]    3   10    2    8
## [3,]    4   15    4    4

##      [,1] [,2] [,3] [,4]
## [1,]    1    0 -2.0   16
## [2,]    0    1  0.8   -4
## [3,]    0    0  0.0    0

A basis for $\mathrm{Col}(A)$ is \[ \begin{bmatrix} 1 \\ 3 \\ 4 \end{bmatrix}, \quad \begin{bmatrix} 5 \\ 10 \\ 15 \end{bmatrix}. \]

A basis for $\mathrm{Nul}(A)$ is \[ \begin{bmatrix} 2 \\ -0.8 \\ 1 \\ 0 \end{bmatrix}, \quad \begin{bmatrix} -16 \\ 4 \\ 0 \\ 1 \end{bmatrix}. \]

29.3.8

A =  cbind(c(1,-1,-2),c(2,-1,1),c(-1,-1,-8))
A

##      [,1] [,2] [,3]
## [1,]    1    2   -1
## [2,]   -1   -1   -1
## [3,]   -2    1   -8

rref(A)

##      [,1] [,2] [,3]
## [1,]    1    0    3
## [2,]    0    1   -2
## [3,]    0    0    0

No they are not a basis. The corresponding matrix only has two pivots. Let’s add the three elementary vectors to create matrix $B$ and then row reduce.

B =  cbind(A, c(1,0,0),c(0,1,0),c(0,0,1))
B

##      [,1] [,2] [,3] [,4] [,5] [,6]
## [1,]    1    2   -1    1    0    0
## [2,]   -1   -1   -1    0    1    0
## [3,]   -2    1   -8    0    0    1

rref(B)

##      [,1] [,2] [,3] [,4]       [,5]       [,6]
## [1,]    1    0    3    0 -0.3333333 -0.3333333
## [2,]    0    1   -2    0 -0.6666667  0.3333333
## [3,]    0    0    0    1  1.6666667 -0.3333333

From this matrix, we can see that the vectors \[ \begin{bmatrix} 1 \\ -1 \\ -2 \end{bmatrix}, \quad \begin{bmatrix} 2 \\ -1 \\ 1 \end{bmatrix}, \quad \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}. \] are linearly independent because they correspond to the basis columns of $B$.

29.3.9

A basis for $\mathbb{R}^5$ is \[ \begin{bmatrix} 5\\ 4\\ 3\\ 1\\ 2 \end{bmatrix}, \begin{bmatrix} 4\\ 4\\ 3\\ 1\\ 2 \end{bmatrix}, \begin{bmatrix} 1\\ 1\\ 1\\ 1\\ 1\end{bmatrix}, \begin{bmatrix} 0\\ 1\\ 0\\ 0\\ 0\end{bmatrix}, \begin{bmatrix} 0\\ 0\\ 1\\ 0\\ 0 \end{bmatrix} \]

because these are basic columns in the given matrix. This will always work: place your desired vectors in the first columns. Since they are linearly independent, they will be basic columns. The remaining $n$ elementary basis vectors span $. So the columns of the matrix span $\mathbb{R}^n$ and Gaussian Elimination will identify $n$ pivots. The corresponding columns are a basis.

29.3.10

We need the matrices \[ P_{\cal B} = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \end{bmatrix} \qquad \mbox{and} \qquad P_{\cal B}^{-1} = \begin{bmatrix} 1 & -1 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 1 &-1 \\ 0 & 0 & 0 & 1 \end{bmatrix} \] The desired coordinate vectors are \[ \mathsf{w} = \begin{bmatrix} 0 \\ -3 \\ -1 \\ -1 \end{bmatrix}_{\mathcal{S}}, \qquad \mathsf{v} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}_{\mathcal{B}} \] Here is the R code for this solution:

A =  cbind(c(1,0,0,0),c(1,1,0,0),c(1,1,1,0),c(1,1,1,1))
Ainv = solve(A)

A  %*% c(3,-2,0,-1)

##      [,1]
## [1,]    0
## [2,]   -3
## [3,]   -1
## [4,]   -1

Ainv %*% c(10,9,7,4)

##      [,1]
## [1,]    1
## [2,]    2
## [3,]    3
## [4,]    4

29.3.11

$\dim(S) = 3$ and a basis for $S$ is \[ \begin{bmatrix} 1 \\ 1 \\ 0 \\ -1 \\2 \end{bmatrix}, \quad \begin{bmatrix} 0 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix}, \quad \begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \\1 \end{bmatrix}. \]
$\dim(\mathrm{Nul}(A))=2$ and a basis is \[ \begin{bmatrix} -3 \\ 2 \\ 1 \\ 0 \\0\end{bmatrix}, \quad \begin{bmatrix} -1 \\ 2 \\ 0 \\ -1 \\1 \end{bmatrix}. \]

29.3.12

$\mathrm{Col}(A)$ has dimension 5, and it is a subspace of $\mathbb{R}^6$. You would find a basis by taking the pivot columns of $A$.
$\mathrm{Nul}(A)$ has dimension 3, and it is a subspace of $\mathbb{R}^8$. You would find a basis by finding the parametric solution to $A \mathsf{x}= \mathbb{0}$.