Vector 2 Problem Set 2
- Due: Friday November 6 by 5:00pm CST.
- Upload your solutions to Moodle in a PDF.
- Please feel free to use RStudio for all row reductions.
- You can download the Rmd source file for this problem set.
The Problem Set covers sections 1.3, 1.4, 1.5.
2.1 Parametric Vector Form
Here is the augmented matrix for a system of linear equations \(\mathsf{A} \mathsf{x} = \mathsf{b}\), and its RREF. Give the complete solution to this system in parametric vector form.
\[\left[ \begin{array}{ccccc|c} 1 & 1 & -1 & -1 & 2 & 1 \\ 1 & 0 & -2 & 1 & 1 & 3 \\ -2 & 1 & 5 & 1 & -6 & 2 \\ -3 & 0 & 6 & 2 & -8 & 1 \\ 0 & 1 & 1 & 2 & -3 & 6 \\ 1 & 0 & -2 & -1 & 3 & -1 \\ \end{array} \right] \longrightarrow \left[ \begin{array}{ccccc|c} 1 & 0 & -2 & 0 & 2 & 1 \\ 0 & 1 & 1 & 0 & -1 & 2 \\ 0 & 0 & 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \right] \]
2.2 RREF for a linear system
Here is the reduced row echelon form of a matrix \(\mathsf{A}\) (you are not given the matrix \(\mathsf{A}\)). \[ \mathsf{A} \longrightarrow \left[ \begin{array}{cccc} 1 & -2 & 0 & 4 \\ 0 & 0 & 1 & -5 \\ 0 & 0 & 0 & 0 \\ \end{array} \right] \]
Give the parametric equations of the general solution to the homogenous equation \(\mathsf{A} \mathsf{x} = {\bf 0}\).
Describe the geometric form of your answer to part (a). For example, you answer should be something like: “it is a plane in \(\mathbb{R}^3\)” or “it is a line in \(\mathbb{R}^7\)” or “it is a point in \(\mathbb{R}^4\).”
Suppose that we also know that \(\mathsf{A}\begin{bmatrix} 4 \\ 1 \\ -3 \\ 2 \\ \end{bmatrix} = \begin{bmatrix} 22 \\ -13 \\ 7 \\ \end{bmatrix}\). Then give the general solution to \(\mathsf{A} \mathsf{x}= \begin{bmatrix} 22 \\ -13\\ 7 \\ \end{bmatrix}\) in parametric form.
2.3 RREF for a set of vectors
Suppose that we have five vectors \(\mathsf{v}_1, \mathsf{v}_2,\mathsf{v}_3,\mathsf{v}_4,\mathsf{v}_5\) in \(\mathbb{R}^4\) and that the matrix \[ A = \left[ \begin{array}{ccc} \mid & \mid & \mid & \mid & \mid \\ \mathsf{v}_1 & \mathsf{v}_2 & \mathsf{v}_3 &\mathsf{v}_4 &\mathsf{v}_5 \\ \mid & \mid & \mid & \mid & \mid \end{array} \right] \] has reduced row echelon form \[ \begin{bmatrix} 1 & 0 & -3 & 0 & 2 \\ 0 & 1 & 4 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}. \]
Do the vectors \(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3, \mathsf{v}_4, \mathsf{v}_5\) span \(\mathbb{R}^4\)? Justify your answer.
Is the vector \(\mathsf{v}_3\) in \(\mathrm{span}(\mathsf{v}_1,\mathsf{v}_2)\)? Justify your answer.
Pick any \(\mathsf{b}\) in \(\mathrm{span}(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3, \mathsf{v}_4, \mathsf{v}_5)\). Is there always a unqiue way to write \(\mathsf{b}\) as a linear combination of \(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3, \mathsf{v}_4, \mathsf{v}_5\)? Justify your answer.
2.4 Removing free variable columns from a matrix
Consider the matrix
\[ A =\left[ \begin{array}{cccccc} 6 & 5 & -3 & 4 & 2 & -9 \\ -7 & -6 & 4 & -5 & -7 & 16 \\ -4 & -3 & -1 & 0 & -8 & 9 \\ 8 & 7 & -5 & 6 & 1 & -12 \end{array} \right]. \]
- Use RStudio to show that the columns of \(\mathsf{A}\) span \(\mathbb{R}^4\).
- Write down matrix \(\mathsf{A}'\) that you get by removing the free variable columns from \(\mathsf{A}\).
- Without using additional calculations on RStudio, explain why the new system \(\mathsf{A}' \mathsf{x} = \mathsf{b}\) is consistent and has a unique solution for every choice of \(\mathsf{b} \in \mathbb{R}^4\).
2.5 A square matrix
Suppose that \(A\) is a \(5\times 5\) matrix and \(\mathsf{b}\) is a vector in \(\mathbb{R}^5\) with the property that \(A\mathsf{x}=\mathsf{b}\) has a unique solution. Explain why the columns of \(A\) must span \(\mathbb{R}^5\). Use the reduced row echelon form of \(A\) in your explanation.
2.6 Combining solutions to \(A \mathsf{x} = \mathsf{b}\)
Suppose that \(\mathsf{x}_1\) and \(\mathsf{x}_2\) are solutions to \(\mathsf{A} \mathsf{x} = \mathsf{b}\) (where \(\mathsf{b} \not= \mathsf{0}\)).
- Decide if any of the following are also solutions to \(\mathsf{A} \mathsf{x} = \mathsf{b}\).
- \(\mathsf{x}_1+ \mathsf{x}_2\)
- \(\mathsf{x}_1 - \mathsf{x}_2\)
- \(\frac{1}{2} ( \mathsf{x}_1 + \mathsf{x}_2)\)
- \(\frac{5}{2} \mathsf{x}_1 - \frac{3}{2} \mathsf{x}_2\).
- Under what conditions on \(c\) and \(d\) is \(\mathsf{x} = c \mathsf{x}_1 + d \mathsf{x}_2\) a solution to \(\mathsf{A} \mathsf{x} = \mathsf{b}\)? Justify your answer.
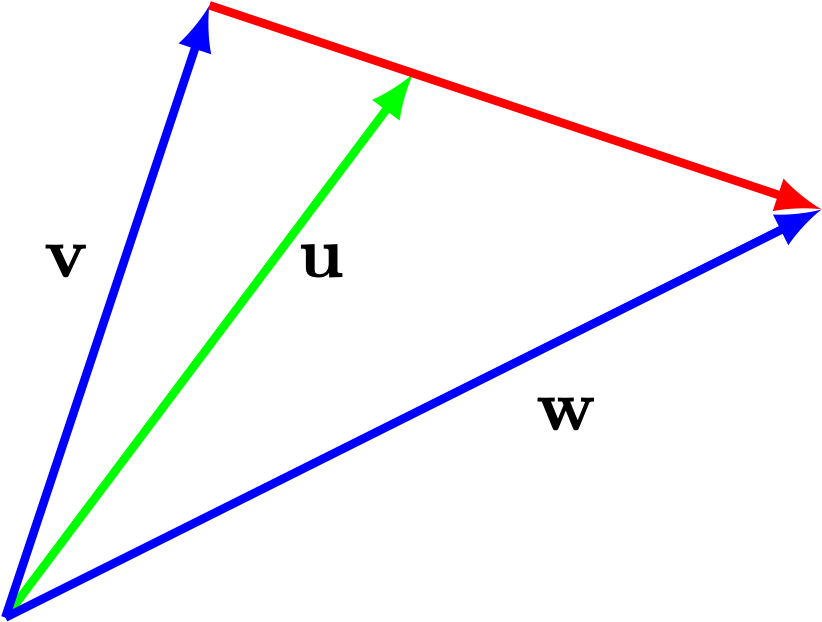
- Let \(\mathsf{u}\) be the vector that points to \(1/3\) of the way from the tip of \(\mathsf{v}\) to the tip of \(\mathsf{w}\) as depicted below.
- Write \(\mathsf{u}\) as a linear combination of \(\mathsf{v}\) and \(\mathsf{w}\) (hint: think about \(\mathsf{w} - \mathsf{v}\))
- If \(\mathsf{v}\) and \(\mathsf{w}\) are solutions to \(A x = \mathsf{b}\) then show that \(\mathsf{u}\) is also a solution to \(A \mathsf{x} = \mathsf{b}\).