Vector 28 Quiz 1 Review

28.1 Overview

Our first quiz covers sections 1.1 - 1.9 in Lay’s book. This corresponds to Problem Sets 1,2,3.

28.1.1 Vocabulary and Concepts

You should understand these concepts and be able to read and use these terms correctly:

  • elementary row operations
  • REF and RREF
  • pivot position
  • linear combination
  • span
  • linear independence
  • homogeneous and nonhomogeneous equations
  • Understand the geometric relationship between the solutions to \(Ax = 0\) and \(Ax=b\)
  • Understand Theorem 4 in Section 1.4 which says that the following are equivalent (they are all true or are all false) for an \(m \times n\) matrix \(A\)
    • For each \(b\) in \(\mathbb{R}^m\), \(A x = b\) has a solution
    • Each \(b\) in \(\mathbb{R}^m\) is a linear combination of the columns of \(A\)
    • The columns of \(A\) span \(\mathbb{R}^m\)
    • \(A\) has a pivot in every row.
  • The columns of \(A\) are linearly independent if and only if \(Ax=0\) only has the trivial solution
  • Understand Theorem 8 in Section 1.7: if you have more than \(n\) vectors in \(\mathbb{R}^n\) they must be linearly dependent.
  • linear transformation
  • one-to-one and onto
  • Understand Theorem 12 in Section 1.9 which states that
    • \(T(x)=Ax\) is onto if and only if the column of \(A\) span \(\mathbb{R}^m\)
    • \(T(x)=Ax\) is one-to-one if and only if the columns of \(A\) are linearly independent.

28.1.2 Skills

You should be able to perform these linear algebra tasks.

  • Identify linear systems from nonlinear systems
  • Make the augmented matrix from a set of equations
  • Row reduce a system of equations into Row Echelon Form (REF) and Reduced Row Echelon Form (RREF)
  • Write the solution set to \(Ax=b\) as a parametric vector equation.
  • Convert back and forth between systems of equations, vector equations, and matrix equations.
  • Compute the matrix-vector product \(Ax\)
  • Determine whether a set of vectors is linearly dependent or independent
  • Find a dependence relation among a set of vectors
  • Decide if a set of vectors span \(\mathbb{R}^n\)
  • Manipulate matrix vector products using: \(A(x + y) = Ax + Ay\) and \(A(c x) = c A x\)
  • Determine whether a linear transformation is one-to-one and/or onto
  • Find the standard matrix for a linear transformation
  • Give geometric descriptions of linear transformations \(T: \mathbb{R}^2 \rightarrow \mathbb{R}^2\)

28.2 Practice Problems

28.2.1

I have performed some row operations below for you on a matrix \(A\). Write out the complete set of solutions to \(A \mathsf{x} = {\bf 0}\). \[ A= \begin{bmatrix} 1& 2& 0& 2& 0& -1 \\ 1& 2& 1& 1& 0& -2 \\ 2& 4& -2& 6& 1& 2 \\ 1& 2& 0& 2& -1& -3 \\ \end{bmatrix} \longrightarrow \begin{bmatrix} 1& 2& 0& 2& 0& -1\\ 0& 0& 1& -1& 0& -1\\ 0& 0& 0& 0& 1& 2\\ 0& 0& 0& 0& 0& 0\\ \end{bmatrix} \]

28.2.2

I have performed some row operations below for you on a matrix \(B\). \[ B= \begin{bmatrix} 1& 1& 0 \\ 0& 1& 1 \\ 2& 1& 2 \\ 1& -1& 1 \\ 2& 3& 1 \\ \end{bmatrix} \longrightarrow \begin{bmatrix} 1& 0& 0 \\ 0& 1& 0 \\ 0& 0& 1 \\ 0&0&0 \\ 0&0&0 \\ \end{bmatrix} \] a. Describe the solutions to the equation \(B \mathsf{x} = {\bf 0}\).

  1. Fill in the boxes: the transformation \(T(\mathsf{x}) = B\mathsf{x}\) is a linear transformation from \(\mathbb{R}^{\square}\) to \(\mathbb{R}^{\square}\).

28.2.3

I want to know if it is possible to write \(\mathsf{w}\) as a linear combination of the vectors \(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3\) below. Write down, but do not solve, a matrix equation that would solve this problem. Your answer should be of the form \(A \mathsf{x} = \mathsf{b}\), where I can clearly see what \(A, \mathsf{x}\), and \(\mathsf{b}\) are. I should also be able to tell how many unknowns there are. \[ \mathsf{v}_1 = \left[ \begin{matrix} 1 \\ 2 \\ 3 \\ 4 \\ \end{matrix}\right] , \quad \mathsf{v}_2 = \left[ \begin{matrix} 1 \\ 0 \\ 1 \\ 0 \\ \end{matrix}\right] , \quad \mathsf{v}_3 = \left[ \begin{matrix} 1 \\ 1 \\ 0 \\ -2 \\ \end{matrix}\right] , \quad \mathsf{w} = \left[ \begin{matrix} 1 \\ -8 \\ -11 \\ -24 \\ \end{matrix}\right] . \]

28.2.4

Describe all vectors that are not in the span of the columns of the matrix \(A\) below: \[ A= \begin{bmatrix} 1& 2& 4 \\ -3& -5& -11\\ 1& 1& 3 \\ \end{bmatrix} \]

28.2.5

The matrix below is \(3 \times 3\) but the third column is missing. Add a nonzero third column so that the columns of \(A\) are linearly dependent and add a 3rd column so that the columns of \(A\) are linearly independent. Briefly describe your strategy. \[ \begin{bmatrix} 1& 0 & \quad \\ 0& 1& \quad \\ 2& 2& \quad \\ \end{bmatrix} \qquad\qquad \begin{bmatrix} 1& 0 & \quad \\ 0& 1& \quad \\ 2& 2& \quad \\ \end{bmatrix} \]

28.2.6

In each case below, find the matrix of the linear transformation that is described, if you believe that the matrix exists. Otherwise, demonstrate that the transformation is not linear.

  1. The transformation \(T\) is given by: \[T \left( \begin{bmatrix} x_1 \\ x_2 \\ \end{bmatrix}\right) = \begin{bmatrix} x_1 + x_2 \\ 2 x_1 \\ -x_2 \\\end{bmatrix}. \]

  2. The transformation \(T\) is given by: \[T \left( \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \right)= \begin{bmatrix} x_1 + x_2 + x_3 \\ x_1 x_2 \\ -x_2 + 2 x_3 \end{bmatrix}. \]

    1. The transformation \(L: \mathbb{R}^2 \to \mathbb{R}^2\) sends the shaded region on the left to the the shaded region on the right such that \(A\) maps to \(A\), \(B\) maps to \(B\), \(C\) maps to \(C\), and \(D\) maps to \(D\).

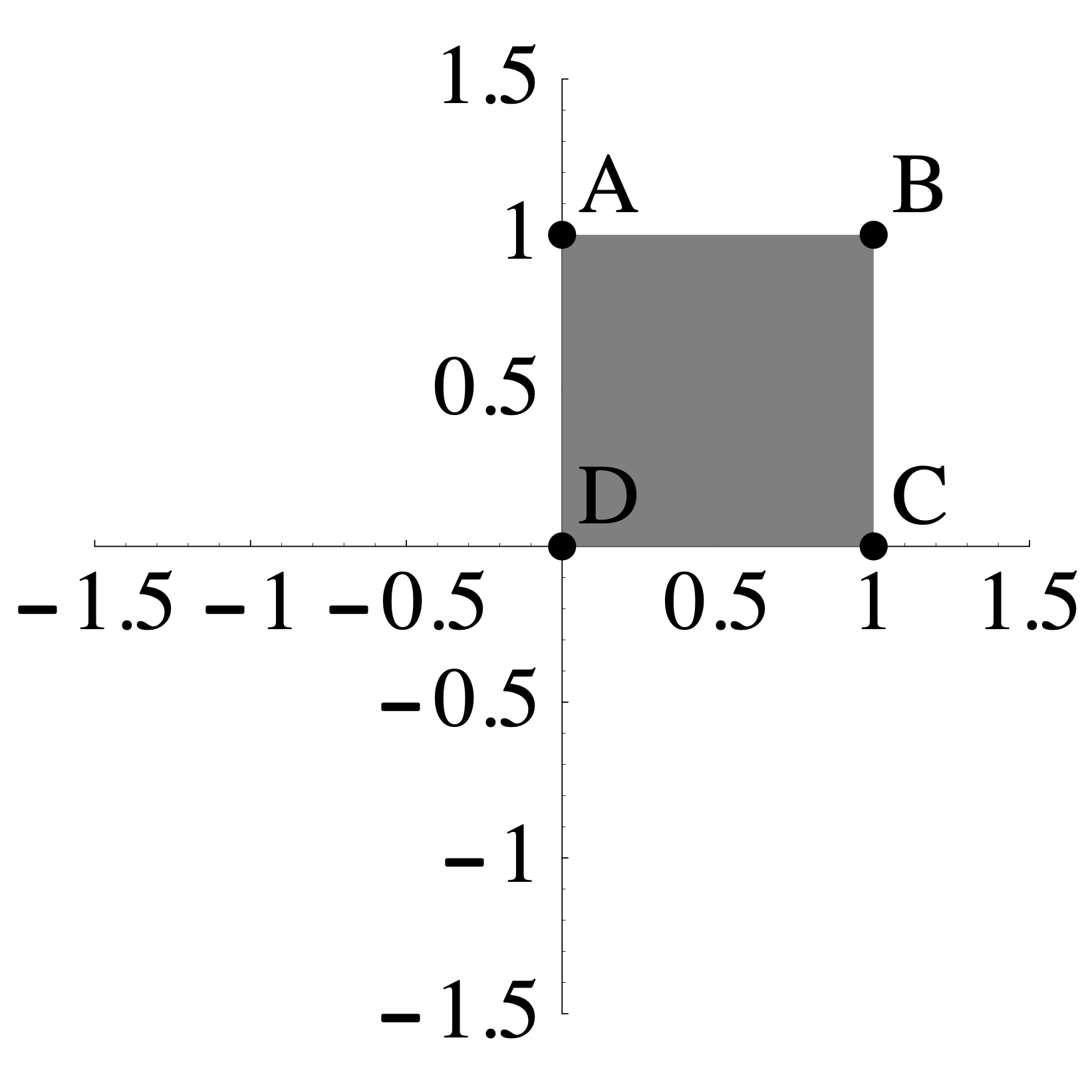\(\qquad \qquad\)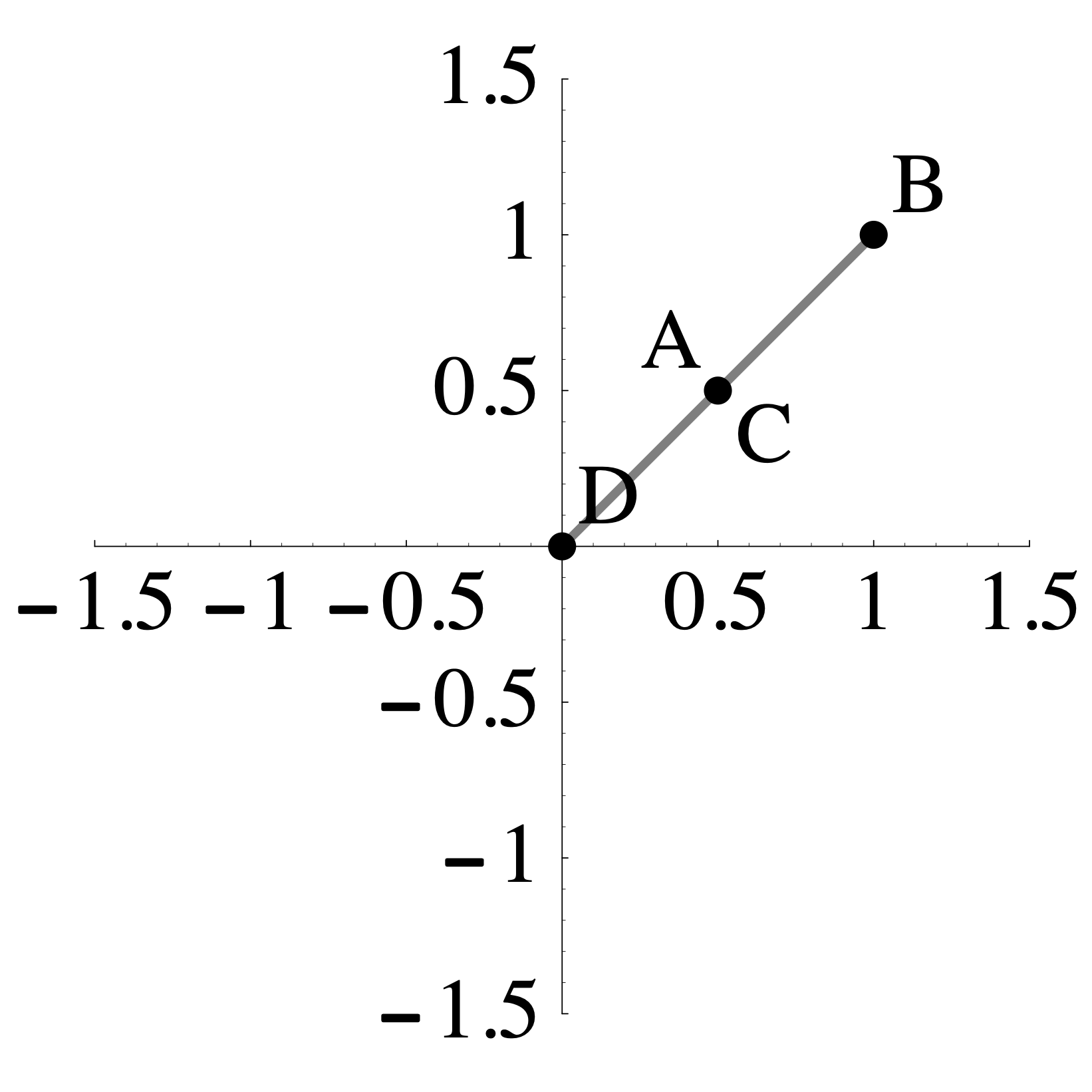

  1. The transformation \(R: \mathbb{R}^2 \to \mathbb{R}^2\) sends the shaded region on the left to the the shaded region on the right such that \(A\) maps to \(A\), \(B\) maps to \(B\), \(C\) maps to \(C\), and \(D\) maps to \(D\).

\(\qquad \qquad\)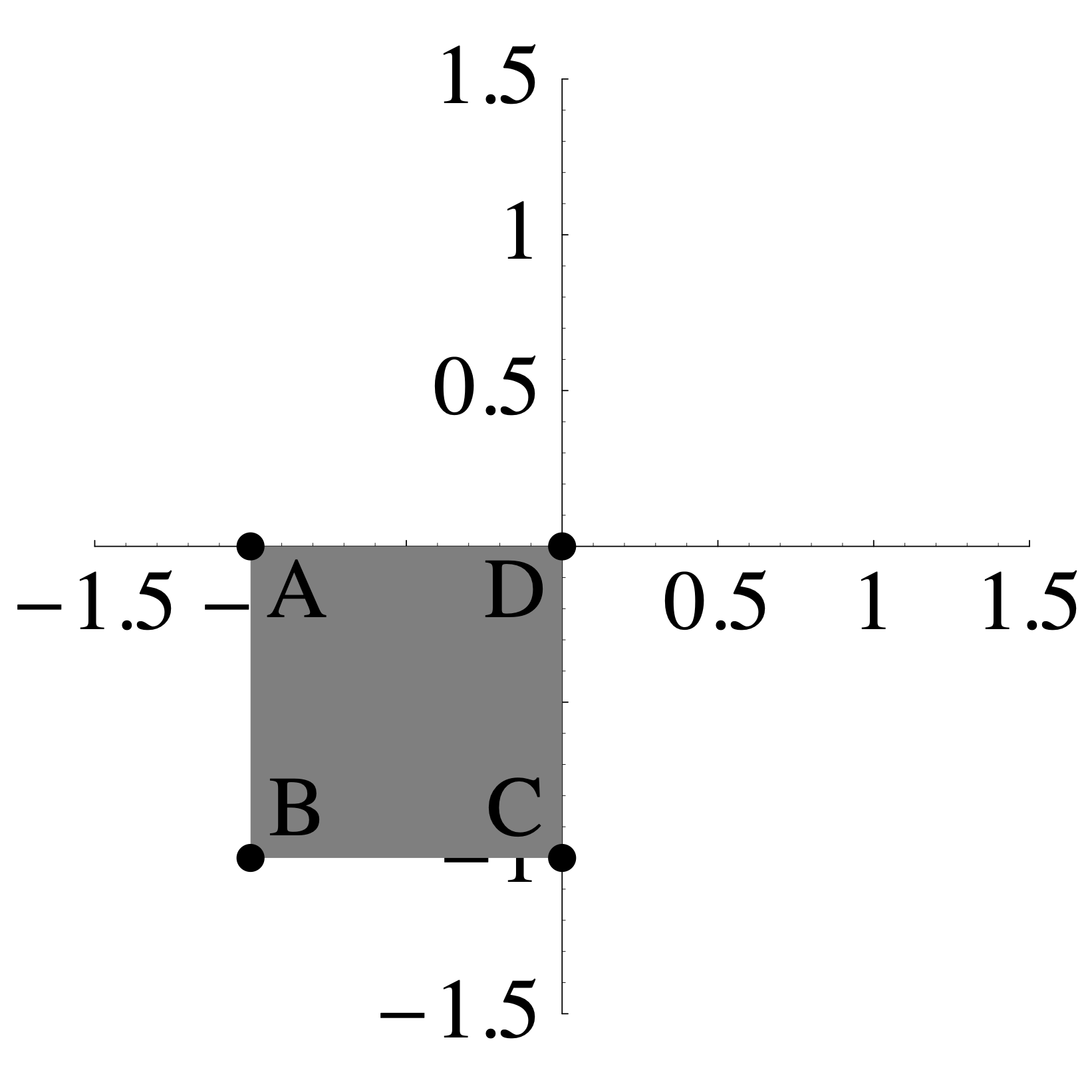

28.2.7

Write the following systems of equations in vector and matrix form.

\[ \begin{array} {ccccccccccc} 5 x_1 &+& 3 x_2 &+& x_3 &+& 11 x_4 &-& x_5 &=& 10 \\ 4 x_1 &+& x_2 &+& 3 x_3 &+& 2 x_4 &+& 6 x_5 &=& 11 \\ - x_1 &+& 3 x_2 &-& 2 x_3 &+& x_4 &+& 6 x_5 &=& 12 \\ \end{array} \]

28.2.8

Let \(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3, \mathsf{v}_4\) be the vectors in the columns of the matrix \(A\) below. \[ A = \left[ \begin{array}{cccc} 1 & 1 & 3 & 1 \\ 2 & 0 & 2 & 3 \\ 1 & 1 & 3 & 1 \\ -1 & 0 & -1 & 0 \end{array} \right] \longrightarrow \left[ \begin{array}{cccc} 1 & 0 & 1 & 0 \\ 0 & 1 & 2 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right] \] a. Are the vectors \(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3, \mathsf{v}_4\) linear independent or dependent? If they are linearly dependent, please give a dependence relation among them. b. Describe the span of the vectors \(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3, \mathsf{v}_4\) inside of \(\mathbb{R}^4\)?

28.2.9

Find a solution to \(A \mathsf{x}=0\) that no one else in the class has. \[ A = \begin{bmatrix} 1 & 1 & 1 & 1 & 4 \\ 2 & 0 & 4 & 1 & 4 \\ 1 & 1 & 1 & 1 & 4 \\ 1 & 0 & 2 & 1 & 3 \end{bmatrix} \longrightarrow \begin{bmatrix} 1 & 0 & 2 & 0 & 1 \\ 0 & 1 & -1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} \]

28.2.10

Let \(T: \mathbb{R}^n \to \mathbb{R}^m\) be a linear transformation. Let \(\mathsf{u}, \mathsf{v}, \mathsf{w}\) be a linearly independent set in \(\mathbb{R}^n\), and suppose that \(T(\mathsf{u}), T(\mathsf{v}), T(\mathsf{w})\) is a linearly dependent set in \(\mathbb{R}^m\).

  1. State precisely what it means for \(T(\mathsf{u}), T(\mathsf{v}), T(\mathsf{w})\) to be linearly dependent.
  2. Use the properties of a linear transformation to demonstrate that \(T(\mathsf{x}) = \mathbf{0}\) has a nontrivial solution.

28.3 Solutions to Practice Problems

28.3.1

The parametric vector form of the solution is

\[\begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ \end{bmatrix} = s \begin{bmatrix} -2 \\ 1 \\ 0 \\ 0 \\0 \\ 0 \end{bmatrix} + t \begin{bmatrix} -2 \\ 0 \\ 1 \\ 1 \\0 \\ 0 \end{bmatrix} u \begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \\-2 \\ 1 \end{bmatrix}\]

28.3.2

  1. There is one solution: \(\mathsf{x} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}\).
  2. The transformation \(T(\mathsf{x}) = B\mathsf{x}\) is a linear transformation from \(\mathbb{R}^{3}\) to \(\mathbb{R}^{5}\).

28.3.3

\[ \begin{bmatrix} 1 & 1 & 1 \\ 2 & 0 & 1 \\ 3 & 1 & 0 \\ 4 & 0 & -2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 1 \\ -8 \\ -11 \\ -24 \end{bmatrix} \]

28.3.4

We want to find all target vectors \(\mathsf{b}\) such that \(A \mathsf{x} = \mathsf{b}\) is inconsistent. So we want the augmented matrix \(\begin{bmatrix} A \,| \, b \end{bmatrix}\) to have a pivot in the last column. \[ \left[ \begin{array}{ccc|c} 1& 2& 4 & b_1 \\ -3& -5& -11 & b_2\\ 1& 1& 3 & b_3 \\ \end{array} \right] \longrightarrow \left[ \begin{array}{ccc|c} 1& 2& 4 & b_1 \\ 0& 1& 1 & 3b_1 +b_2\\ 0& -1& -1 & -b_1+b_3 \\ \end{array} \right] \longrightarrow \left[ \begin{array}{ccc|c} 1& 2& 4 & b_1 \\ 0& 1& 1 & 3b_1 +b_2\\ 0& 0& 0 & 2b_1+b_2+b_3 \\ \end{array} \right] \] So the set of target vectors that are not in the span of the columns of \(A\) are the vectors \[ \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} \qquad \mbox{where} \qquad 2b_1 + b_2 + b_3 \neq 0. \]

28.3.5

There are lots of right answers to this one. In my first matrix, I will just add the first two columns to get the thrid column. Then I will add one to one to the bottom right entry of the matrix. \[ \begin{bmatrix} 1& 0 & 1 \\ 0& 1& 1 \\ 2& 2& 4 \\ \end{bmatrix} \qquad\qquad \begin{bmatrix} 1& 0 & 1 \\ 0& 1& 1 \\ 2& 2& 5 \\ \end{bmatrix} \]

28.3.6

  1. This is a linear transformation with \[A = \begin{bmatrix} 1 & 1 \\ 2 & 0 \\ 0 & -1 \end{bmatrix}.\]

  2. This is not a linear transformation because \[ 2 \, T \left( \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \right)= 2 \begin{bmatrix} 3 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 6 \\ 2 \\ 2 \end{bmatrix} \quad \mbox{while} \quad T \left( \begin{bmatrix} 2 \\ 2 \\ 2 \end{bmatrix} \right)= 2 \begin{bmatrix} 6 \\ 4 \\ 2 \end{bmatrix}. \]

  3. \(A= \begin{bmatrix} 1/2 & 1/2 \\ 1/2 & 1/2 \end{bmatrix}\)

  4. \(A= \begin{bmatrix} 0 & -1 \\ -1 & 0 \end{bmatrix}\)

28.3.7

Vector Form: \[ x_1 \begin{bmatrix} 5 \\ 4 \\ -1 \end{bmatrix} + x_2 \begin{bmatrix} 3 \\ 1 \\ 3 \end{bmatrix} + x_3 \begin{bmatrix} 1 \\ 3 \\ -2 \end{bmatrix} + x_4 \begin{bmatrix} 11 \\ 2 \\ 1 \end{bmatrix} + x_5 \begin{bmatrix} -1 \\ 6 \\ 6 \end{bmatrix} = \begin{bmatrix} 10 \\ 11 \\ 12 \end{bmatrix} \] Matrix Form: \[ \begin{bmatrix} 5 & 3 & 1 & 11 & -1 \\ 4 & 1 & 3 & 2 & 6 \\ -1 & 3 & -2& 1 & 6 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{bmatrix} = \begin{bmatrix} 10 \\ 11 \\ 12 \end{bmatrix} \]

28.3.8

  1. \(-\mathsf{v}_1 - 2\mathsf{v}_2 + \mathsf{v}_3 + 0 \mathsf{v}_4 = 0\).
  2. \(\mathrm{span}(\mathsf{v}_1,\mathsf{v}_2,\mathsf{v}_3,\mathsf{v}_4)\) looks like a copy of \(\mathbb{R}^3\) sitting inside \(\mathbb{R}^4\). In other words, is 3-dimensional subset of \(\mathbb{R}^4\).

28.3.9

The general solution is \[ \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{bmatrix} = s \begin{bmatrix} -2 \\ 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} + t \begin{bmatrix} -1 \\ -1 \\ 0 \\ -2 \\ 1 \end{bmatrix}. \] My solution is \[77,083,679 \begin{bmatrix} -2 \\ 1 \\ 1 \\ 0 \\ 0 \end{bmatrix} - 72,159,215 \begin{bmatrix} -1 \\ -1 \\ 0 \\ -2 \\ 1 \end{bmatrix}. \]

28.3.10

  1. There are scalars \(c_1, c_2, c_3\) not all zero such that \(c_1 T(\mathsf{u}) + c_2 T(\mathsf{v}) + c_3 T(\mathsf{w}) = \mathbf{0}\).
  2. We have \[ \mathbf{0} = c_1 T(\mathsf{u}) + c_2 T(\mathsf{v}) + c_3 T(\mathsf{w}) = T(c_1 \mathsf{u} + c_2 \mathsf{v}+ c_3 \mathsf{w}) \] However, we know that \(\mathsf{u}, \mathsf{v},\mathsf{w}\) are linearly independent, so \[ c_1 \mathsf{u} + c_2 \mathsf{v}+ c_3 \mathsf{w} \neq \mathbf{0}. \] This is a nonzero vector that maps to the zero vector. Therefore \(T\) is not one-to-one.