Vector 3 Problem Set 3

  • Due: Tuesday November 10 by 11:55pm CST.
  • Upload your solutions to Moodle in a PDF.
  • Please feel free to use RStudio for all row reductions.
  • You can download the Rmd source file for this problem set.

The Problem Set covers sections 1.7, 1.8, 1.9.

3.1 Three vectors in \(\mathbb{R}^4\)

Consider the vectors \(\mathbf{u}\), \(\mathbf{v}\), and \(\mathbf{w}\) given by \[ \qquad \mathbf{u} = \begin{bmatrix} 1 \\ 0 \\ 2 \\ -1 \end{bmatrix}, \qquad \mathbf{v} = \begin{bmatrix} 2 \\ -1 \\ 3 \\ 1 \end{bmatrix}, \qquad \mathbf{w} = \begin{bmatrix} 1 \\ -2 \\ 2 \\ 1 \end{bmatrix}. \] Use RStudio to answer the following questions.

  1. Are \(\mathbf{u}\), \(\mathbf{v}\), and \(\mathbf{w}\) linearly independent?

  2. Is the vector \(\mathbf{b} = \begin{bmatrix} 4 \\ 4 \\ 2 \\ 4 \end{bmatrix}\) in the span of vectors \(\mathbf{u}\), \(\mathbf{v}\), and \(\mathbf{w}\)?

  3. Is the vector \(\mathbf{b} = \begin{bmatrix} 2 \\ 1 \\ 3 \\ 1 \end{bmatrix}\) in the span of vectors \(\mathbf{u}\), \(\mathbf{v}\), and \(\mathbf{w}\)?

3.2 A Balanced Diet

An athlete wants to consume a daily diet of 200 grams of carbohydrates, 60 grams of fats and 160 grams of proteins. Here are some of their favorite foods.

Table 3.1: Food Carb/Fat/Protein (grams)
food carbs fats proteins
almonds 3 8 5
avocado 15 31 4
beans 20 1 8
bread 12 1 2
cheese 1 5 3
chicken 0 13 50
egg 1 5 6
milk 12 8 8
zucchini 6 0 2

Answer the following questions, using RStudio for your calculations. Each response must use two or more of the following terms: linear combination, span, linearly dependent, linearly independent.

  1. Explain why they cannot achieve their daily goal by eating only almonds, milk and zucchini.

  2. Explain why they cannot achieve their daily goal by eating only almonds, beans and cheese.

  3. Find a valid one-day diet consisting of almonds, chicken, and zucchini.

3.3 A Problem about Span and Linear Dependence

Let \(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3\) and \(\mathsf{w}_1, \mathsf{w}_2, \mathsf{w}_3, \mathsf{w}_4\) all be vectors in \(\mathbb{R}^4\). Suppose that \(\{ \mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3 \}\) is a linearly independent set, and that \[ \mathrm{span}(\mathsf{v}_1, \mathsf{v}_2, \mathsf{v}_3) = \mathrm{span}(\mathsf{w}_1, \mathsf{w}_2, \mathsf{w}_3, \mathsf{w}_4). \] Prove that \(\mathsf{w}_1, \mathsf{w}_2, \mathsf{w}_3, \mathsf{w}_4\) must be linearly dependent. You can do this by either:

  • Explaning why there must be a nontrivial linear combination \(c_1 \mathsf{w}_1 + c_2 \mathsf{w}_2 + c \mathsf{w}_3 + c \mathsf{w}_4 = \mathbf{0}\), or
  • Showing that the \(4 \times 4\) matrix \(\begin{bmatrix} \mathsf{w}_1 & \mathsf{w}_2 & \mathsf{w}_3 & \mathsf{w}_4 \end{bmatrix}\) does not have a pivot in every column.

3.4 Properties of Linear Transformations

Here are the row reductions to reduced row echelon form of 4 matrices. \[ \begin{array}{ll} A \longrightarrow \begin{bmatrix} 1 & 0 & 5 & -3 & 0\\ 0 & 1 & -2 & 8 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} \qquad & B \longrightarrow \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix} \\ \\ C \longrightarrow \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} & D \longrightarrow \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \end{bmatrix} \end{array} \]

In each case, if \(T\) is the linear transformation given by the matrix product \(T(x) = M x\), where \(M\) is an \(m \times n\) matrix (\(m\) rows and \(n\) columns) then \(T: \mathbb{R}^n \to \mathbb{R}^m\) is a transformation from domain \(\mathbb{R}^n\) to codomain (aka target) \(\mathbb{R}^m\).

Determine the appropriate values for \(n\) and \(m\), and decide whether \(T\) is one-to-one and/or onto. Submit your answers in table form, as shown below. \[ \begin{array} {|c|c|c|c|c|} \hline \text{matrix } M & n & m & \text{one-to-one?} & \text{onto?} \\ \hline A &\phantom{\Big\vert XX}&\phantom{\Big\vert XX}&& \\ \hline B &\phantom{\Big\vert XX}&&& \\ \hline C &\phantom{\Big\vert XX}&&& \\ \hline D &\phantom{\Big\vert XX}&&& \\ \hline \end{array} \hskip5in \]

3.5 Partial Information about a Linear Transformation

\(T: \mathbb{R}^4 \rightarrow \mathbb{R}^3\) is a linear transformation such that: \[ T\left(\begin{bmatrix} 1 \\ 2 \\ 2 \\ 0 \end{bmatrix} \right) = \begin{bmatrix} ~4~ \\ -1~ \\ 2 \end{bmatrix} \quad \mbox{and} \quad T\left(\begin{bmatrix} 2 \\ -1~ \\ 1 \\ 3 \end{bmatrix} \right) = \begin{bmatrix} ~2~ \\ 6 \\ -1~ \end{bmatrix} \quad \mbox{and} \quad T\left(\begin{bmatrix} 3 \\ 0 \\ 2 \\ 2 \end{bmatrix} \right) = \begin{bmatrix} 6 \\ 5 \\ 1 \end{bmatrix} \]

  1. Do we have enough information to determine whether \(T\) is one-to-one? If no, then explain why not. If yes, then do so, along with a justification.

  2. Do we have enough information to determine whether \(T\) is onto? If no, then explain why not. If yes, then do so, along with a justification.

3.6 House Renovations

Find the matrix of a linear transformation \(T: \mathbb{R}^2 \to \mathbb{R}^2\) that performs the given transformation of my house. (Hint: use the base, the doorway and the peak of the roof as a guide.)

  1. Transformation #1

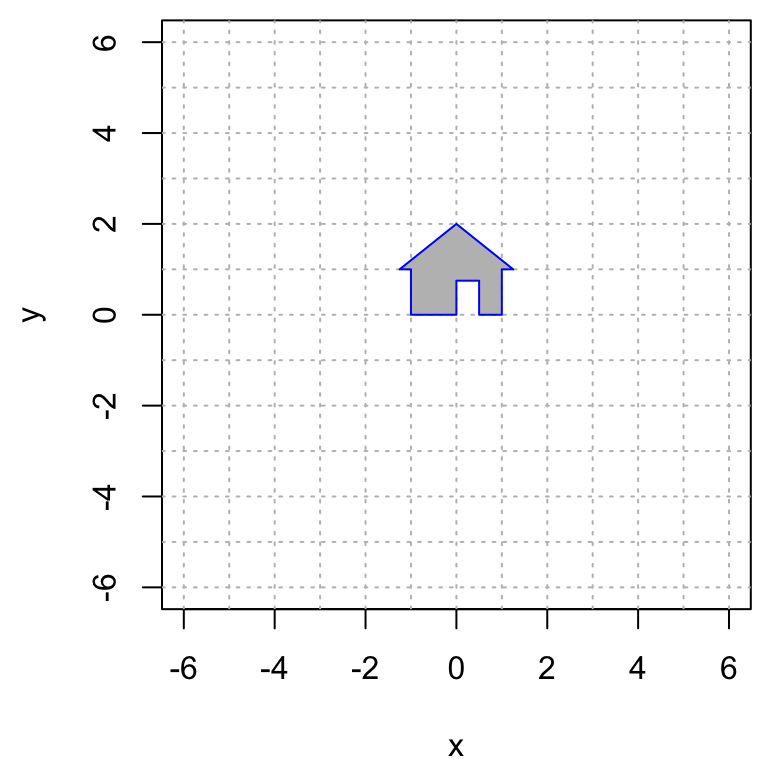\(\qquad \qquad\)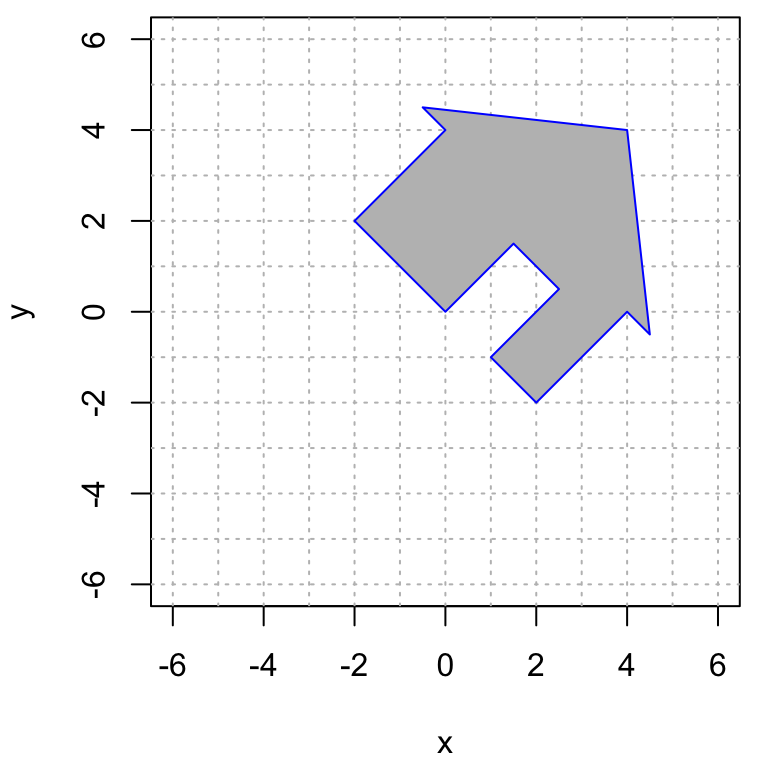

  1. Transformation #2

\(\qquad \qquad\)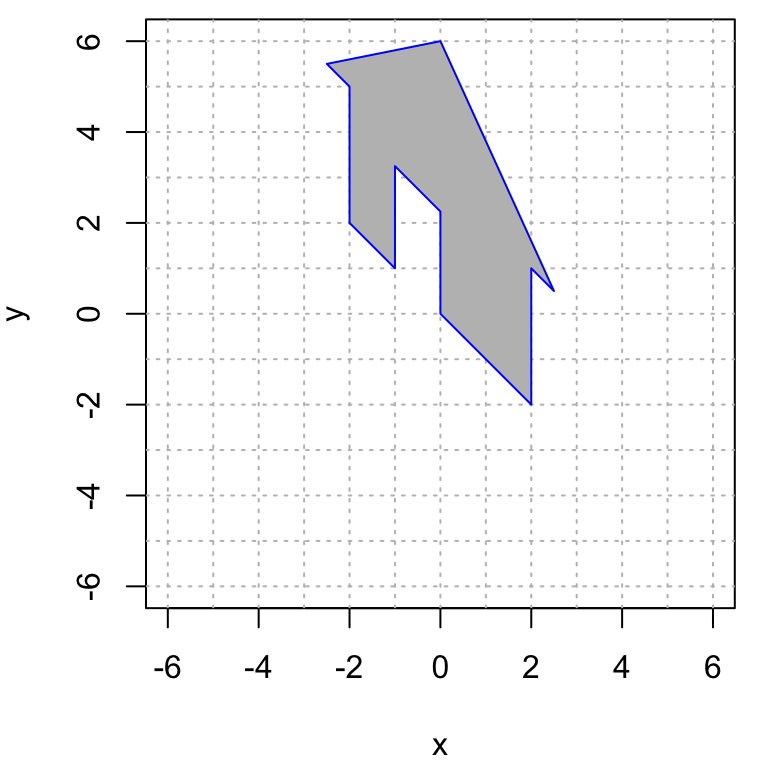

For your convenience, here is the code to make the original plot of the house.

par(pty="s")
house = cbind(c(0,0), c(0,3/4), c(1/2,3/4), c(1/2,0), c(1,0), c(1,1), c(5/4,1), c(0,2), c(-5/4,1), c(-1,1), c(-1,0), c(0,0));

plot(house[1,],house[2,],type="n",xlim=c(-6,6),ylim=c(-6,6),xlab="x",ylab="y", asp=1)
abline(h=-6:6, v=-6:6, col="gray", lty="dotted")
polygon(house[1,], house[2,], col = "gray", border = "blue")