Vector 6 Problem Set 6
- Due: Friday December 04 by 11:55pm CST.
- Upload your solutions to Moodle in a PDF.
- Please feel free to use RStudio for all calculations, including row reduction, matrix multiplication, eigenvector calculation and inverse matrices.
- You can download the Rmd source file for this problem set.
The Problem Set covers sections 5.1, 5.2, 5.3, 5.5 and Network Analysis.
6.1 The Square Root of a Matrix?
The matrix \(A =\begin{bmatrix} 7 & 2 \\ -4 & 1 \end{bmatrix}\) has characteristic polynomial \(\lambda^2 - 8 \lambda + 15 = (\lambda -3)(\lambda - 5).\)
- Describe the eigenspaces of \(A\).
- Diagonalize \(A\).
- Find a matrix that makes sense to call \(\sqrt{A}\). Then show that when you square this matrix, you really do get matrix \(A\).
6.2 A Matrix Mystery
An unknown \(3 \times 3\) matrix \(M\) has eigenvectors and corresponding eigenvalues: \[ \mathsf{v}_1 = \begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix}, \ \lambda_1 = 1; \qquad \mathsf{v}_2 = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix},\ \lambda_2 = \frac{9}{10}; \qquad \mathsf{v}_3 = \begin{bmatrix} -1 \\ 1 \\ 0 \end{bmatrix},\ \lambda_3 = 0. \]
Find (exactly, if possible, or approximately otherwise) the vector \(M^{10} \mathsf{v}\) where \(\mathsf{v} = \begin{bmatrix}7\\3\\4\end{bmatrix}\).
Describe all vectors \(\mathsf{v}\), if there are any, such that \(M^{n} \mathsf{v} \to {\bf 0}\) as \(n \to \infty\).
Is it possible to reconstruct \(M\) from the evidence given? If so, then do it! If not, explain what further information is needed.
6.3 Upper Triangular Matrix with a Constant Diagonal
Let \(A\) be a \(3 \times 3\) upper triangular matrix of the form \[ A = \begin{bmatrix} d & a & b \\ 0 & d & c \\ 0 & 0 & d \end{bmatrix} \] where \(d \neq 0\) and at least one of \(a,b,c\) is nonzero. Explain why \(A\) is not diagonalizable.
6.4 Block Diagonalization of a \(4 \times 4\) Matrix
The \(4 \times 4\) matrix \[ A = \begin{bmatrix} 2 & -1 & 1 & -1 \\ 1 & -3 & 3 & 2 \\ 2 & -9 & 7 & 0 \\ 2 & -4 & 2 & 0 \end{bmatrix} \] has complex eigenvalues \(a \pm bi\) and \(c \pm di\).
Use RStudio to find the eigenvalues \(a \pm bi\) and \(c \pm di\), as well as “human friendly” eigenvectors
- \(\mathsf{v} = \mathsf{v}_1 + i \mathsf{v}_2\) for eigenvalue \(a + bi\), and
- \(\mathsf{w} = \mathsf{w}_1 + i \mathsf{w}_2\) for eigenvalue \(c + di\).
Hint: the command
zapsmall()might be helpful.This matrix A can be factored as \(A = P B P^{-1}\) where \(B\) is a “block diagonal” matrix of the form \[ B = \begin{bmatrix} a & -b & 0 & 0 \\ b & a & 0 & 0 \\ 0 & 0 & c & -d \\ 0 & 0 & d & c \end{bmatrix} \] and \[ P = \begin{bmatrix} \mathrm{Im} (\mathsf{v}) & \mathrm{Re} (\mathsf{v}) & \mathrm{Im} (\mathsf{w}) & \mathrm{Re}( \mathsf{w}) \end{bmatrix} =\begin{bmatrix} \mathsf{v}_2 & \mathsf{v}_1 & \mathsf{w}_2 & \mathsf{w}_1 \end{bmatrix} \] where the constants \(a,b,c,d\) and the vectors \(\mathsf{v}, \mathsf{w}\) are as described in part (a). Use RStudio to find the \(4 \times 4\) matrices \(B\), \(P\) and its inverse \(P^{-1}\).
Hints:
- You can use the command
solve(M)to find the inverse of matrix \(M\). - You can confirm that your answer is correct by computing \(P B P^{-1}\) and checking that this equals the original matrix \(A\).
- You can use the command
6.5 Network Analysis of Risk Territories
Risk is a classic board game of conflict and diplomacy played on a map of the world. Players try to capture territories by moving their armies through adjancent territories. Here is what the game map looks like, with the countries colored by continent.

Risk Game Board (image: wikipedia)
Here is a network representation of the gameboard, created from an adjacency matrix.
library(igraph)
risk <- read.csv("https://raw.github.com/mathbeveridge/math236_f20/main/data/riskmatrix.csv")
A = data.matrix(risk)
countries = names(risk)
g=graph_from_adjacency_matrix(A,mode='undirected')
coords = layout_nicely(g)
plot(g, layout=coords, vertex.size = 10, vertex.label.cex=0.75, vertex.color='khaki', vertex.frame.color="black")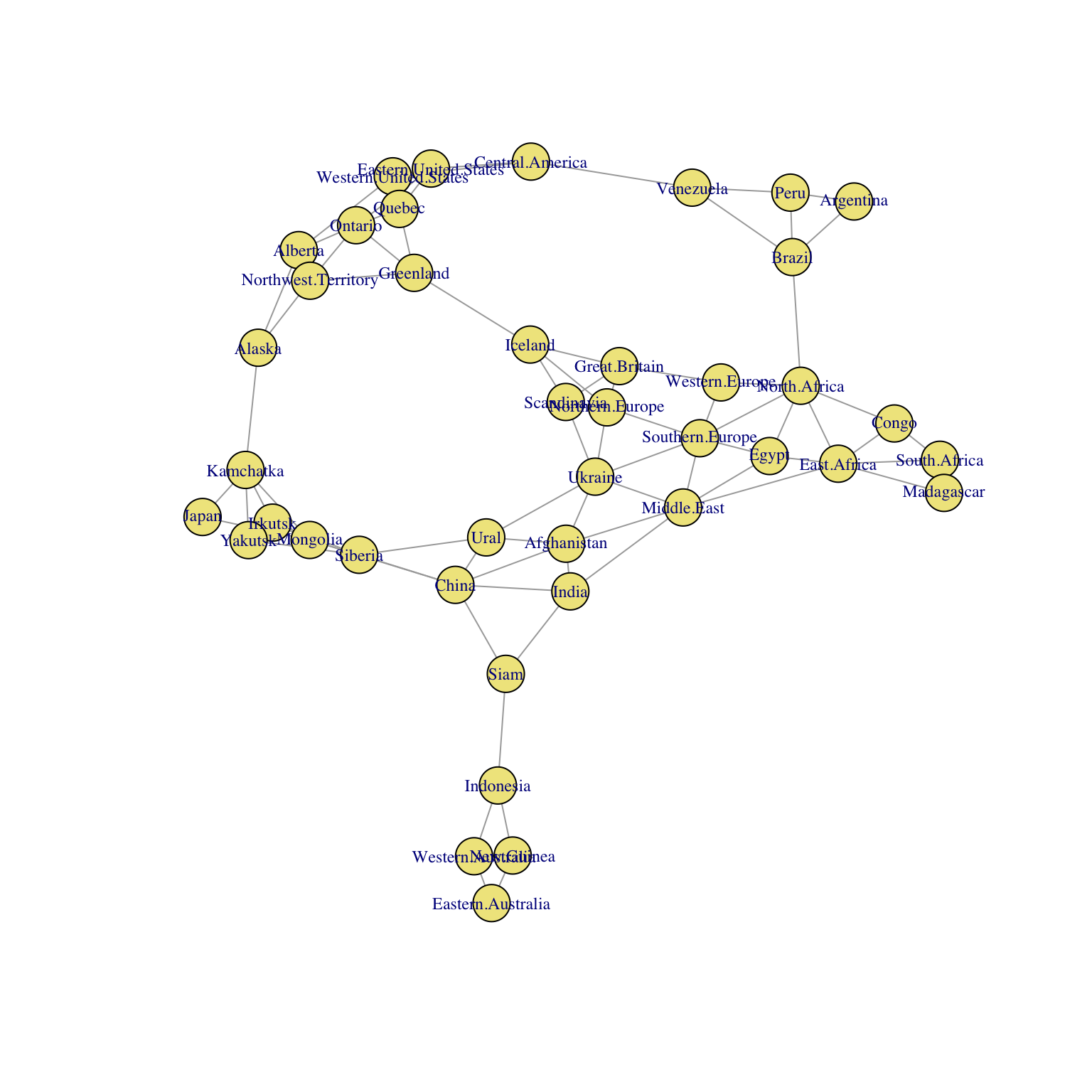
Calculate Gould’s Index for this network. Use this Gould’s Index ranking to identify the most central territory in each of the six continents in this worldwide network. Here is a list of territories by continent (Africa, Asia, Australia, Europe, North America, South America) to help you to classify the territories.
Turn in a table with six rows. These six rows should be ordered by Gould’s index. Each row should contain:
- name of the continent
- name of the territory with the largest Gould Index,
- the degree of the territory,
- the Gould’s Index value for the territory.
Important: You do not need to show your work for this problem! Just turn the table (handwritten is fine) of your results.