Enumerative Combinatorics: Activities and Exercises

1. Cycles in a permutation.

1. Prove that \(\displaystyle{c(n) = \sum_{k=1}^n k \cdot c(n,k)}\text{.}\) Solution.

   The LHS is the total number of cycles in all \(n\)-permutations. Consider the \(k\)th term of the RHS: \[ \underbrace{c(n,k)}_{\​begin{array}{c}\mbox{# permutations} \\ \mbox{with \(k\) cycles} \end{array}} \cdot \underbrace{k}_{\​begin{array}{c}\mbox{# cycles in such} \\ \mbox{a permutation} \end{array}} \] We sum over \(1 \leq k \leq n\) to get all possibilities.

2. Prove that \(\displaystyle{A(n) = \frac{c(n)}{n!}}\text{.}\) Solution.

   Dividing \(c(n)\) by the total number of permutations yields \(A(n)\text{.}\)

2. The Harmonic Numbers.

1. Use a graph to explain why \(H(n)\) is a pretty good approximation for \(\int_1^n \frac{1}{x} dx\text{.}\) What function does this integral represent? Solution.

   

   The integral \(\int_1^n \frac{1}{x} dx\) can be approximated by the sum \(1 + \frac{1}{2} + \frac{1}{3} + \cdots \frac{1}{n}\) as shown in the above graph.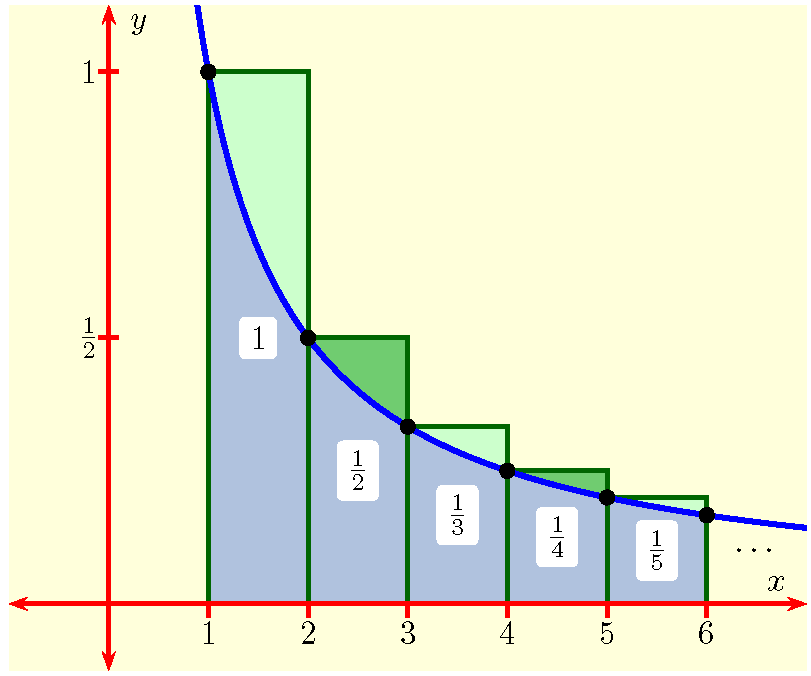

   Evaluating this integral gives \(\int_1^n \frac{1}{x} dx = \log (n) - \log (1) = \log n\) where \(\log(x)\) is the natural logarithm of \(x\text{.}\)

2. Interpret the meaning of \(A(n) = \sum_{i=1}^n \frac{1}{i}\) using your approximate function. Solution.

   The average number of cycles in an \(n\)-permutation is approximately \(\log n\text{.}\)

3. A recurrence for \(c(n)\).

We will prove the recurrence

As usual, we will treat element \(n\) as special. Given an \(n\)-permutation \(f \in S_n\text{,}\) what happens when we remove element \(n\text{?}\) There are two cases

1. Suppose that \(n\) was in a cycle by itself. Prove that the total number of cycles in such permutations is \(c(n-1) + (n-1)!\text{.}\) Solution.

   When \(n\) is in a cycle by itself, the permutation naturally corresponds to an \((n-1)\)-permutation. There are \(c(n-1)\) cycles in all such permutations. We add \((n-1)!\) to account for final the cycle containing \(n\) because there are \((n-1)!\) permutations of \([n-1]\text{.}\)

2. Suppose that \(n\) was not in a cycle by itself. Prove that the total number of cycles in such permutations is \((n-1) \cdot c(n-1)\text{.}\) Solution.

   Removing \(n\) from the permutation gives an \((n-1)\)-permutation with the same number of cycles. We obtain each \((n-1)\) cycle in \(n-1\) ways, since the element \(n\) can be placed before any element of the \((n-1)\)-permutation (and within the same cycle as that element).

Putting together the answers from questions 2 and 3, we find that

as claimed at the start of the problem.

4. The main result.

Starting with the formula in problem 1(b) and the recurrence in problem 2, prove that

Solution.