Skip to main content

Chapter 12 Recursive Sequences

Exercises Practice Problems

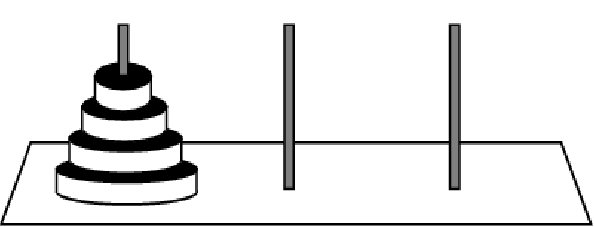
1. Towers of Hanoi.

The Towers of Hanoi puzzle has three rods (\(A\text{,}\) \(B\text{,}\) and \(C\)) and \(n\) disks. The disks are stacked in decreasing value of diameter on rod A. The objective of the puzzle is to move the entire stack to rod \(C\text{,}\) obeying the rules:

  • Only one disk can be moved at a time.

  • Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack.

  • No disk may be placed on top of a smaller disk.

Use induction to prove that you can solve the Towers of Hanoi puzzle with \(n\) disks in \(2^n-1\) moves.

Solution.

  • Base Case: A Tower of Hanoi with 1 disk can be solved in \(1 = 2^1 -1\) moves.

  • Inductive Hypothesis: Assume that a Tower of Hanoi with \(k\) disks can be solved in \(2^k -1\) moves.

  • Inductive Step: Prove that a Tower of Hanoi with \(k+1\) disks can be solved in \(2^{k+1} -1\) moves.

    By induction, we can move \(k\) disks from \(A\) to \(B\) in \(2^k-1\) moves. We then move the largest disk to \(C\) in 1 move. Finally, we move \(k\) disks from \(B\) to \(C\) in \(2^k-1\) moves. The total number of moves is

    \begin{equation*} (2^k-1) + 1 + (2^k -1) = 2^{k+1} -1. \end{equation*}
2. An Oddly Recursive Sequence.

Define a number sequence as follows: let \(a_0=1\text{,}\) \(a_1=3\text{,}\) and let \(a_n=2a_{n-1}-a_{n-2}\) for all \(n \geq 2\text{.}\) Prove, using strong induction, that \(a_n=2n+1\) for all \(n \in \mathbb{N}.\)

Solution.

  • Base Case: We have \(a_0=1\) and \(a_1=3\) and \(a_2 = 2a_1-a_0=6-1=5= 2 \cdot 2 + 1\text{.}\)

  • Inductive Hypothesis: Assume that \(a_k = 2k+1\text{.}\)

  • Inductive Step: Prove that \(a_{k+1} = 2(k+1)+1=2k+3\text{.}\)

    We have, by strong induction,

    \begin{gather*} a_{k+1} = 2 a_{k} - a_{k-1} = 2(2k+1) - (2(k-1)+1) = 4k + 2 - 2k +2 - 1 \\ = 2k+3 = 2(k+1)+1. \end{gather*}
3. Fibonacci Fun.

The Fibonacci numbers are defined by \(F_1=1, F_2=2\text{,}\) and \(F_n=F_{n-1}+F_{n-2}\) for all \(n \geq 3\text{.}\)

  1. Prove that \(F_1 + F_2 + F_3 + \ldots + F_n = F_{n+2}-2\) for all \(n \geq 1\text{.}\) Solution.

    • Base Case: We have \(F_1=1\) and \(F_3-2=3-2=1\text{.}\)

    • Inductive Hypothesis: Assume that \(F_1 + F_2 + F_3 + \ldots + F_k = F_{k+2}-2\text{.}\)

    • Inductive Step: Prove that \(F_1 + F_2 + F_3 + \ldots + F_{k+1} = F_{k+3}-2\text{.}\)

      We have, by strong induction,

      \begin{gather*} F_1 + F_2 + F_3 + \ldots + F_k + F_{k+1} = F_{k+2}-2 + F_{k+1} = F_{k+3} -2. \end{gather*}

  2. Prove that \(F_1 + F_3 + F_5 + \ldots + F_{2n-1} = F_{2n} - 1\) for all \(n \geq 1\text{.}\) Solution.

    • Base Case: We have \(F_1=1\) and \(F_2-1=2-1=1\text{.}\)

    • Inductive Hypothesis: Assume that \(F_1 + F_3 + F_5 + \ldots + F_{2k-1} = F_{2k}-1\text{.}\)

    • Inductive Step: Prove that \(F_1 + F_3 + F_5 + \ldots + F_{2k+1} = F_{2k+2}-1\text{..}\)

      We have, by strong induction,

      \begin{gather*} F_1 + F_3 + F_5 + \ldots + F_{2k-1} + F_{2k+1} = F_{2k}-1 + F_{2k+1} = F_{2k+2} -1. \end{gather*}