Discrete Mathematics: Activities and Exercises

1. Our First Graph.

A graph is a set \(V\) of vertices and a set \(E\) of edges connecting pairs of points. By convention, we denote the number of vertices by \(n=|V|\) and the number of edges by \(m = |E|\text{.}\)

Here is an example. The vertices are points and the edges are lines connecting pairs of points.

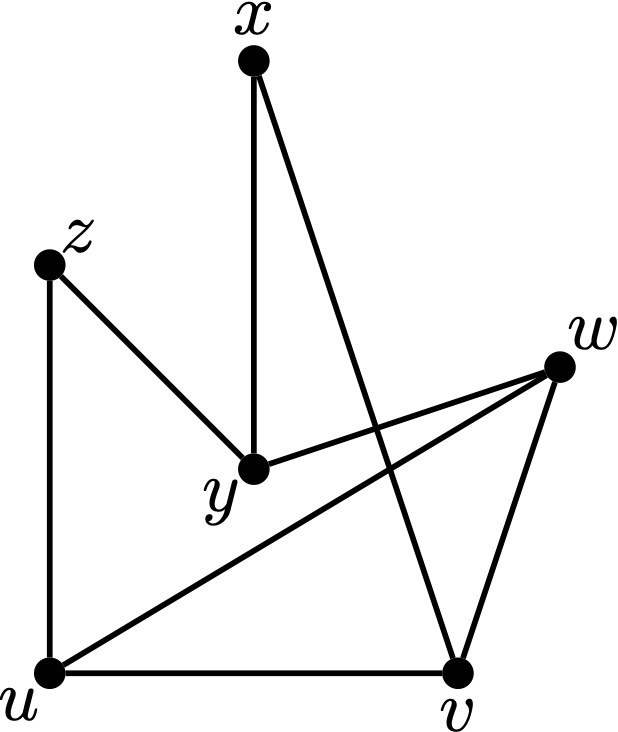
• \((u,v)\) is an edge that is incident with both \(u\) and \(v\text{.}\) Therefore, \(u\) and \(v\) are adjacent.

• \((x,w)\) is not an edge

• \(w\) is incident with 3 edges, so its degree is \(\deg(w)=3\text{.}\)

1. What are the degrees of the vertices of \(G\text{?}\) Solution.

   \begin{equation*} \deg(u)=3 \deg(v)=3 \deg(w)=3 \deg(x)=2 \deg(y)=3 \deg(z)=2 \end{equation*}

2. The graph \(G\) is drawn so that some of the edges are crossing, meaning that they intersect. For example, edge \(e_1 = (x,v)\) crosses edge \(e_2 = (y,w)\text{.}\) Create another drawing of the graph \(G\) so that none of the edges are crossing. Solution.

   

3. The complement \(\overline{G}\) of graph \(G\) is the "graph of edges missing in \(G\text{.}\)" It has the same vertices as \(G\text{.}\) But the edge \((u,v) \in E(\overline{G})\) if and only if \((u,v) \notin E(G)\text{.}\) Draw the complement \(\overline{G}\) of the graph \(G\text{.}\) Can you draw \(\overline{G}\) so that none of its edges are crossing? Solution.

   

2. Families of Graphs.

1. Paths. The path \(P_n\) is the graph consisting of a path on \(n\) vertices.

   
   How many edges are there in \(P_n\) for \(n \geq 2\text{?}\) Solution.

   \(n-1\)

2. Cycles. The cycle \(C_n\) is the graph corresponding to a closed walk on \(n\) vertices whose only repetition is the first/last vertex.

   
   How many edges are there is the cycle \(C_n\) for \(n \geq 3\text{?}\) Solution.

   \qquad \(n\)

3. Wheels. The wheel \(W_n\) is the graph consisting of a cycle \(C_{n-1}\) along with a single hub node that is adjacent with each node in that cycle.

   
   How many edges are there in the wheel \(W_n\) for \(n \geq 4\text{?}\) Solution.

   \((n-1) + (n-1) = 2n-2\)

4. Complete Graphs. The complete graph \(K_n\) is the graph on \(n\) vertices with every possible edge.

   
   How many edges are there in the complete graph \(K_n\) for \(n \geq 2\text{?}\) Solution.

   \(n(n-1)/2\)

5. Complete Bipartite Graphs. The complete bipartite graph \(K_{r,s}\) is the graph whose vertices are divided into sets \(A\) and \(B\text{,}\) where \(|A|=r\) and \(|B|=s\text{.}\) Every vertex in \(A\) is adjacent to every vertex in \(B\text{.}\) There are no other edges.

   
   How many edges are there in the complete bipartite graph \(K_{r,s}\) for \(r \geq 1\) and \(s \geq 1\text{?}\) Solution.

   \(rs\)

3. Counting edges and degrees.

Let \(G = (V,E)\) be a graph on \(n\) vertices with \(m\) edges.

1. The Handshaking Lemma. Prove that

   \begin{equation*} \sum_{v \in V} \deg(v) = 2|E|. \end{equation*}

   This is our first example of a "combinatorial identity": you are counting the same set in two different ways. This equality is known as "the handshaking lemma." Solution.

   When we sum the degrees, we count each edge twice. So the left hand side is equal to 2 times the number of edges.

2. Prove that the number of vertices of odd degree is even. First, partition \(V\) into two sets: the vertices of odd degree and the vertices of even degree. Then use the handshaking lemma (from the previous problem). Solution.

   Let \(V_{odd}\) be the set of vertices of odd degree and let \(V_{even}\) be the set of vertices of even degree. We have \[ \sum_{v \in V} \deg(v) = \sum_{v \in V_{even}} \deg(v) + \sum_{v \in V_{odd}} \deg(v) . \] By the previous problem, the Left Hand Side is even. Clearly \(\sum_{v \in V_{even}} \deg(v) \) must be even since it the sum of even numbers. This means that \(\sum_{v \in V_{odd}} \deg(v)\) must be even. This will only occur when \(|V_{odd}|\) is even.

3. Prove that if \(G\) is a connected graph on \(n\) vertices then \(G\) contains two vertices that have the same degree. Hint: what are the possible values for \(\deg(v)\) for \(v \in V(G)\text{?}\) Solution.

   For any vertex \(v \in V\text{,}\) we have \(1 \leq \deg(v) \leq n-1\text{.}\) Why? The graph is connected, so \(deg(v) \geq 1\) for each vertex. Meanwhile, the largest possible degree is \(n-1\text{,}\) which means that the vertex is adjacent to every other vertex.

   Now we have \(n\) vertices. There are only \(n-1\) possible values for the degrees, so there must be at least two vertices that have the same degree.

   This argument (\(n\) things with \(n-1\) different types) is an example of the pigeonhole principle. We'll see this kind of argument again!

4. Connected Graphs.

A graph is connected when every pair of vertices are connected by a path in the graph. Any graph is made up of connected components. In other words, we can view any graph as the union of its components, which are themselves connected graphs. Below, we see an example of a connected graph and example of a graph with three components.

1. Let \(G\) be a graph with \(|V|=n\text{.}\)

   1. Suppose \(G\) is connected. Find a lower bound on \(|E|\text{.}\) Start by exploring examples for \(n=2,3,4,5\text{.}\) You do NOT have to prove your answer is correct. Solution.

      The graph must have at least \(n-1\) edges. (A connected tree with exactly \(n-1\) edges is called a tree.)

   2. Suppose that \(G\) is disconnected. Find an upper bound on \(|E|\text{.}\) Start by exploring examples for \(n=2,3,4,5\text{.}\) You do NOT have to prove your answer is correct. Solution.

      A disconnected graph can have a most \((n-1)(n-2)/2\) edges. This occurs when \(G\) is a complete graph on \(n-1\) vertices along with one isolated vertex.

5. Bipartite Graphs.

A graph \(G=(V,E)\) is bipartite if its vertex set can be partitioned into two sets \(A\) and \(B\) such that the only edges in \(G\) run between these two sets. Equivalently: we can color the vertices of a bipartite graph with two colors, red and black, so that adjacent vertices receive different colors. The complete bipartite graph \(K_{n,m}\) is an example of a bipartite graph. Here are some more examples of bipartite graphs.

1. For which values of \(n\) is \(P_{n}\) a bipartite graph? Solution.

   \(P_n\) is always bipartite.

2. For which values of \(n\) is \(C_{n}\) a bipartite graph? Solution.

   \(C_n\) is bipartite if and only if \(n\) is even.

3. For which values of \(n\) is \(W_{n}\) a bipartite graph? Solution.

   \(W_n\) is never bipartite. It has lots of 3-cycles.

4. For which values of \(n\) is \(K_{n}\) a bipartite graph? Solution.

   \(K_2\) is bipartite. If \(n>2\) then \(K_n\) is not bipartite: it has 3-cycles.

5. Suppose that \(G\) is a bipartite graph on \(n\) vertices. Find an upper bound on \(|E|\text{.}\) Start by exploring examples for \(n=2,3,4,5\text{.}\) You do not need to prove your answer is correct. Solution.

   You get the most edges when you split the edges as evenly as possible. So let \(r = \lfloor n/2 \rfloor\) and \(s = \lceil n/2 \rceil\text{.}\) The most number of edges that you get is

   \begin{equation*} rs = \lfloor n/2 \rfloor \times \lceil n/2 \rceil \end{equation*}