Discrete Mathematics: Activities and Exercises

1. Planar Graph Examples.

Fill in the following table for the given connected and planar graphs. Then make a conjecture!

Solution.

2.

Let \(G\) be a connected planar graph with \(v_G\) vertices and \(e_G\) edges and \(f_G\) faces. You will use strong induction on the number of cycles \(k \geq 0\) to prove that any plane drawing of \(G\) satisfies

1. Base Case: \(k=0\). A connected graph with no cycles is a tree. We know that a tree on \(v_G\) vertices has \(v_G-1\) edges. Explain why \(v_G -e_G +f_G = 2.\) Solution.

   A tree on \(n_G\) vertices has \(v_G-1\) edges and 1 region. We have

   \begin{equation*} v_G - (v_G -1) + 1 = 2. \end{equation*}

2. Strong Inductive Hypothesis: Assume that a plane drawing of a connected planar graph \(H\) with fewer than \(k\) cycles satisfies

   \begin{equation*} v_H - e_H + f_H = 2. \qquad \qquad {(\star)} \end{equation*}

3. Inductive Step: Use \((\star)\) to prove that a graph \(G\) with \(k\) cycles satisfies

   \begin{equation*} v_G - e_G + f_G = 2. \end{equation*}

   Start with a plane drawing of \(G\text{.}\) Pick any edge \(e\) that is in a cycle of \(G\text{.}\) Let \(H=G-e\) be the graph you obtain by removing the edge \(e\) (but keeping the vertices).

   1. What can you say about the number of cycles in the graph \(H=G-e\text{?}\)

      We have removed an edge that was part of one or more cycles. So the number of cycles in \(H=G-e\) is strictly smaller than \(k\text{.}\)

   2. What are the following values:

      \begin{equation*} v_H = \qquad \qquad e_H = \qquad \qquad f_H = \end{equation*}

      Solution.

      \begin{equation*} v_H = v_G \qquad \qquad e_H = e_G-1 \qquad \qquad f_H = f_G - 1\qquad \phantom{,} \end{equation*}

      because when we remove the edge \(e\text{,}\) two of the regions merge into one region.

   3. Now complete the inductive step. Solution.

      By induction \((\star)\text{,}\) we know that

      \begin{align*} v_H - e_H + f_H &= 2\\ v_G - (e_G -1) + (f_G -1) &= 2\\ v_G - e_G + f_G &= 2. \end{align*}

3. Adding the lengths of all cycles.

Let \(G\) be a planar graph whose plane drawing has regions \(A_1, A_2, \ldots, A_r\text{.}\) Let \(\mbox{len}(A_i)\) denote the number of steps you take when you walk around the boundary of region \(A_i\text{.}\) Explain why

Start by looking at a small example planar graph to understand what this combinatorial identity is saying. Solution.

4. An upper bound on the number of faces.

Let \(G\) be a simple (no loops, no multiple edges), connected plane graph on \(v \geq 3\) vertices. Use Problem 3 to prove that

Hint: what is a lower bound on the number of edges in the boundary of each region? Solution.

5. An upper bound on the number of edges.

Use the fact that \(v-e+f=2\) and \(3f \leq 2e\) to prove that if \(G\) is a planar graph then

In other words, if \(G\) is planar it cannot have "too many" edges. Solution.

6. \(K_5\) is not planar.

In the previous problem, we showed that for any planar graph, we have \(e \leq 3v-6\text{.}\) Use this inequality to prove that \(K_5\) is not planar. Solution.

7. \(K_{3,3}\) is not planar.

The argument from Problem 5 can be generalized when we know that the planar graph \(G\) does not have any triangles (3-cycles). In this case, we must have

1. Use this inequality to prove that \(K_{3,3}\) is not planar. Solution.

   \(K_{3,3}\) has \(v=6\) vertices and \(e=9\) edges. But \(e = 9 > 8 = 2 \cdot 6 -4\text{.}\) So \(K_{3,3}\) is not planar.

2. Adapt your argument from Problem 5 to prove the following statement.

   Let \(G\) be a simple connected planar graph with \(v\) vertices, \(e\) edges and \(f\) facecs where every face is bounded by at least 4 edges. Prove that \(e \leq 2v -4\text{.}\) Solution.

   Since \(G\) has no 3-cycles, every region is bounded by at least 4 edges. This means that

   \begin{equation*} 4f \leq \sum_{i=1}^r \mbox{len}(A_i) = 2 e, \end{equation*}

   or equivalently,

   \begin{equation*} r \leq \frac{1}{2}e. \end{equation*}

   Plugging this into \(v-e+f = 2\) gives

   \begin{align*} v-e + \frac{1}{2} e &\geq 2\\ v - \frac{1}{2} e &\geq 2\\ v - 2 & \geq \frac{1}{2}e\\ 2v -4 & \geq e. \end{align*}

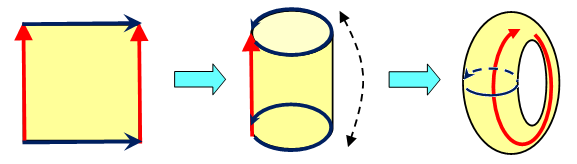
8. Drawing \(K_5\) and \(K_{3,3}\) on a Torus.

If you start with a square and we glue the opposite sides to one another, we get a torus (a surface in the shape of a donut). So we can think of this square as a torus, if we identify points on opposite sides. (For example, in some classic video games, walking off the right side of the screen makes you appear at the same height on the left side of the screen.)