How to Be a Player: Impartial Combinatorial Games

We leave the proof for the exercises.

The proof of the Colon Principle is very similar to the proof of the Tuft Principle (and the Loop Principle, Lemma 4.4.2). Therefore, we leave this proof as an exercise.

The proof of Theorem 4.4.3 is a tour de force of combinatorial game theory. It pulls together all the great themes we have seen up to now. It also requires some new and insightful tools of its own. The overall theme of the proof is a methodical proof by contradiction. In particular, we slowly characterize the structure of a smallest counterexample (also known as a "minimal criminal") and show that no such graph exists.

This sophisticated proof is beyond the level of an introductory textbook. Therefore, we break the proof into two pieces. We lay out the flow of the proof via a series of claims (and then prove these claims later on). This way you can appreciate the overall argument, without getting lost in the details.

The proof methodically places constraints on the structure of the minimal criminal. Eventually, we show that all of these constraints lead to a position that does obey the Fusion Principle. Therefore, there is no minimal criminal, which means that every graph obeys the Fusion Principle.

The Fusion Principle says that we can fuse together some (or all) the vertices in a cycle without changing the Sprague-Grundy value. Let \(\mathcal{A}\) be the set of all counterexamples to the Fusion Principle. Assume for the sake of contradiction that the Fusion Principle is false. This means that \(\mathcal{A} \neq 0\text{.}\) Each graph in \(\mathcal{A}\) contains a particular cycle \(C\) such that if you fuse this cycle, the Sprague-Grundy value changes.

We will restrict ourselves to the subset \(\mathcal{B} \subset \mathcal{A}\) of minimal counterexamples of the Fusion Principle. In other words, if we fuse any cycle in \(G \in \mathcal{B}\text{,}\) then the Sprague-Grundy value changes. Finally, we choose a graph \(G \in \mathcal{B}\) of smallest size: we choose \(G\) so that the sum of the number of vertices and edges in \(G\) achieves the smallest such value among graphs in \(\mathcal{B}\text{:}\)

Choosing this "minimal criminal" \(G\) will be crucial in our proof. Let \(n=|V(G)|\) and \(m=|E(G)|\text{.}\) We prove the following statements, in order.

1. Claim 1: \(G\) has a unique root vertex.

2. Claim 2: \(G\) does not contain any vertices \(x,y\) connected by 3 (or more) edge-disjoint paths.

3. Claim 3: Every cycle of \(G\) must include the unique root vertex.

4. Claim 4: \(G\) contains exactly one cycle through the root vertex.

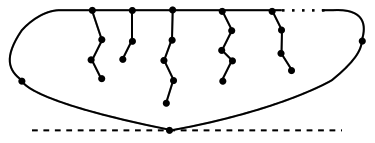
5. Claim 5: \(G\) must look like the graph shown in Figure 4.5.3. This graph consists of a single cycle that includes the ground, along with a number of paths branching off of this cycle.

6. Claim 6: All graphs of the type shown in Figure 4.5.3 obey the Fusion Principle!

Of course, Claim 6 brings us to our contradiction: our (supposed) minimal criminal actually obeys the Fusion Principle. This means that the minimal criminal does not exist, so the set \(\mathcal{A}\) of counterexamples is empty. Therefore the Fusion Principle holds for all graphs.

If \(G\) had multiple vertices at the ground level, we could join them together to get a single vertex without changing the Sprague-Grundy value. This reduces the total number of vertices and edges. Since \(G\) is the minimal criminal, there can only be one root vertex at ground level. \(\quad \Box\)

Assume for the sake of contradiction that \(G\) contains vertices \(x,y\) connected by 3 edge-disjoint paths. Let \(H\) be the graph obtained by merging the vertices \(x\) and \(y\) into a single vertex \(z\text{.}\) We must have \(g(H) \neq g(G)\) because \(G\) is the minimal criminal. Therefore the sum of games \(G \oplus H\) is an \(\cN\)-position.

Since \(G \oplus H\) is an \(\cN\)-position, Left must have a winning move. When Left hacks an edge in \(G\) (or \(H\)), Right responds by hacking the corresponding edge in \(H\) (or \(G\)). Call the resulting graphs \(G'\) and \(H'\text{.}\) Both graphs have \(m-1\) edges, so the fusion principle applies to each of them. The vertices \(x,y\) are still in a cycle in \(G'\) since we can only destroy one of the three edge-disjoint paths between them. So we can fuse \(x\) and \(y\) without changing the Sprague-Grundy value of \(G'\text{.}\) This fusion results in the graph \(H'\text{,}\) so

In other words, \(G' \oplus H'\) is a \(\cP\)-position. No matter what move Left make, Right can make a counter-move to put the game in a \(\cP\)-position. This contradicts the fact that \(G \oplus H\) is an \(\cN\)-position. Therefore, no vertices \(x,y\) can be connected by 3 edge-disjoint paths. \(\quad \Box\)

Assume for the sake of contradiction that \(G\) contains a cycle \(C\) that does not include the unique root vertex \(x\text{.}\)

Let \(P_1\) be a path from \(x\) to \(y \in V(C)\) that does not contain any other vertex of \(C\text{.}\) We claim that every path from \(x\) to \(C\) goes through \(y\text{.}\) Suppose this is not the case. Let \(P_2\) be a path from \(x\) to another vertex \(z \in V(C)\) that does not contain any other vertex of \(C\text{.}\) The walk \(P_1 \cup P_2\) contains a \((y,z)\) path that is edge disjoint from the cycle \(C\text{.}\) Meanwhile, the cycle \(C\) contains two more edge disjoint \((y,z)\) paths (by traversing \(C\) from \(y\) to \(z\) clockwise and counterclockwise, respectively). This contradicts Claim 2. So every path from \(x\) to \(C\) goes through a single vertex \(y\text{.}\) The vertex \(y\) is called a cutpoint since its removal disconnects the graph.

We can now split the graph \(G\) into two subgraphs \(H, K\) at vertex \(y\text{,}\) as shown in Figure 4.5.7. The subgraph \(K\) contains the cycle \(C\text{,}\) and \(K\) contains strictly fewer vertices than \(G\text{.}\) Therefore, the fusion principle applies to \(K\text{.}\) Let \(K'\) be the graph obtained by fusing all of the vertices of \(C\) into one vertex. We have \(\g(K) = \g(K')\) and therefore

by the Colon Principle, Theorem 4.5.2. The resulting graph \([H_y : K']\) has fewer vertices than \(G\text{,}\) so the Fusion Principle applies to \([H_y : K']\text{.}\) But this means that the Fusion Principle also applies to \(G\text{,}\) a contradiction. Therefore, every cycle in our minimal criminal \(G\) must go through the root vertex \(x\text{.}\) \(\Box\)

Let \(C\) be a cycle through the root vertex \(x\text{.}\) Let \(y \in V(C)\text{.}\) By Claim 2, there are exactly two paths from \(y\) to \(x\text{:}\) the clockwise and counterclockwise paths along the cycle \(C\text{.}\) Suppose that \(G\) contained another cycle \(C'\) through the root vertex \(x\text{.}\) The cycles \(C\) and \(C'\) cannot intersect at any other points. Indeed, if \(x \neq z \in V(C) \cap V(C')\) then there would be three edge-disjoint paths between \(x\) and \(z\text{,}\) contradicting Claim 2. Furthermore, any path between \(C\) and \(C'\) must go through \(x\) for the same reason. Therefore, we can view \(G\) as the sum of two smaller graphs. The fusion principle would apply to each of these smaller graphs, a contradiction. Therefore, \(G\) contains exactly one vertex through the root vertex. \(\quad \Box\)

This graph consists of a single cycle that includes the ground, along with a number of paths branching off of this cycle. Putting our first four claims together, we see that \(G\) must consist of a cycle through the root vertex, along with trees branching off of the vertices of this cycle. We can repeatedly use the Colon Principle, Theorem 4.5.2, to turn each of these trees into a path: such replacement cannot increase the number of vertices or edges (and it might actually reduce these numbers). \(\Box\)

We think of this graph as a cycle \(C\) along with a set of dangling paths, which we call strings. Assume for the sake of contradiction that such a graph does not obey the Fusion Principle. In other words: fusing the cycle \(C\) changes the Sprague-Grundy value. There are two cases, depending on the parity of the cycle length. Let the strings of \(G\) have lengths \(n_1, n_2, \ldots, n_k\text{.}\)

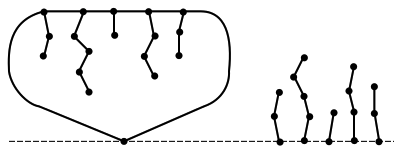
Suppose that \(C\) contains an even number of edges. Consider the sum of games consisting of \(G\) along with a copy of all of the strings, as shown in Figure 4.5.11. We prove that Right has a winning strategy from this position (so it is a \(\cP\)-position). If Left hacks a path edge, Right responds by hacking the analogous edge in the other graph. Left must be the first player to hack an edge in the cycle. This creates a Lumberjack position with an odd number of edges. This position has an odd (and hence nonzero) Sprague-Grundy value by the Parity Principle, Theorem 4.5.1. So Right has a winning strategy from this point forward.

The above argument shows that the position in Figure 4.5.11 is a \(\cP\)-position with Sprague-Grundy value 0. Therefore the Sprague-Grundy value of \(G\) equals

But this means that the Fusion Principle holds for \(G\text{:}\) fusing the cycle \(C\) results in an even number of loops at ground level. These loops cancel one another out, so the Sprague-Grundy value is just the nim sum of the lengths of the strings. In summary, \(G\) is not our minimal criminal.

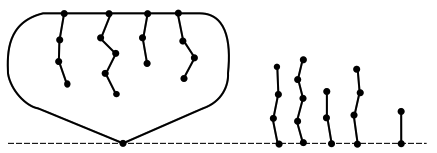
Finally, we rule out the last suspected minimal criminal. This argument gets quite technical, and requires some new ingenuity. Therefore, we only sketch the final steps of this proof. Suppose that \(C\) contains an odd number of edges. This time, we need a more intricate argument. As in the previous case, we consider position \(H\) consisting of \(G\) and copies of each of the strings the cycle of \(G\text{,}\) as shown in Figure 4.5.12. If we can show that \(g(H)=1\text{,}\) then this means that the Fusion Principle holds for \(G\text{,}\) since fusing the cycle creates an odd number of paths of height 1.

We will prove that \(g(H)=1\) by showing that

1. No follower of this position has value 1.

2. There is a follower of value 0

The first statement is straight forward to prove. Hacking the cycle leads to a Lumberjack position with an even number of edges. By the Parity Principle, the Sprague-Grundy value of this position is even, so clearly it cannot be equal to 1. If Left hacks a path edge to obtain position \(G'\text{,}\) then Right responds by hacking the analogous path edge in the other part of the graph to obtain \(G"\text{.}\) The graph \(G"\) has fewer edges than \(G\text{,}\) so the Fusion Principle applies to \(G"\) and its Sprague-Grundy value is 1. This means that \(\g(G') \neq 1\) since its follower \(G"\) has \(\g(G")=1\text{.}\)

Proving that \(G\) has a follower with value 0 is more challenging. It turns out that there is an edge we can hack in the cycle to reach a follower with value 0. We describe how to find such an edge.

Starting clockwise from the root vertex, label each edge with \(\alpha\) or \(\beta\text{,}\) giving adjacent edges the same label if there is an odd length string between them, and different labels if there is an even length string. There are an odd number of edges in \(C\text{,}\) so one label occurs an odd number of times, and the other label occurs an even number of times. For simplicity, we assume that label \(\alpha\) appears an even number of times and that label \(\beta\) appears an odd number of times. It turns out that there exists a \(\beta\)-edge such that hacking this edge results in a position with value 0.

To find this good \(\beta\)-edge, we reduce the graph by picking any edge \(e\) labeled by \(\alpha\) and shrinking it to a single vertex. We replace the two strings from the endpoints of \(e\) by a single string whose length is their nim sum. Next, we halve all of the string lengths of this component (rounding down if this length is odd). Call this resulting graph \(G'\text{.}\) It can be shown that \(\g(G') = \frac{1}{2} \g(G)\text{.}\)

Repeat this process on the graph \(G'\text{:}\) label the edges by \(\alpha'\) and \(\beta'\text{,}\) then contract an edge from the even-sized set of labeled edges and half the sizes of the strings. Continue this process (creating \(G", G"'\text{,}\) etc) until one of the sets of labeled edges contains exactly one edge \(f\) (this must happen eventually). This edge \(f\) is the one that we are looking for: removing the edge \(f\) from the original position results in a composite position with value 0. \(\Box\)